C Program to multiply two matrices

Matrix multiplication is a core operation in linear algebra, essential for various applications in computer graphics, machine learning, and scientific computing. This article will guide you through writing a C program to multiply two matrices, providing a detailed explanation and sample code.

What is Matrix Multiplication?

Matrix multiplication involves combining two matrices to produce a third matrix. If you have matrix A with dimensions m x n and matrix B with dimensions n x p, their product C will be an m x p matrix. Each element C_ij of matrix C is computed as:

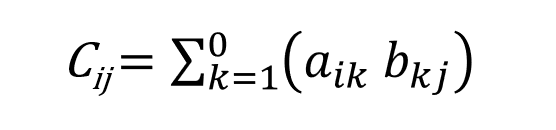
This means that each element of the resulting matrix is the sum of the products of corresponding elements from the rows of the first matrix and columns of the second matrix.

Steps to Multiply Two Matrices

To multiply two matrices in C, follow these steps:

1. Input the Dimensions: Read the dimensions of the matrices from the user.
2. Input the Elements: Read the elements of the two matrices from the user.
3. Initialize the Result Matrix: Create a matrix to store the multiplication result.
4. Perform the Multiplication: Calculate each element of the result matrix using nested loops.
5. Print the Result: Output the resulting matrix to the console.

Write a C Program to multiply two matrices

#include <stdio.h>

int main() {
    int m, n, p;

    // Input the dimensions of the matrices
    printf("Enter the number of rows and columns of the first matrix (m n) -\n");
    scanf("%d %d", &m, &n);

    printf("Enter the number of columns of the second matrix: ");
    scanf("%d", &p);

    // Declare the matrices
    int matrix1[m][n], matrix2[n][p], result[m][p];

    // Input elements of the first matrix
    printf("Enter elements of the first matrix:\n");
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            printf("Element [%d][%d]: ", i, j);
            scanf("%d", &matrix1[i][j]);
        }
    }

    // Input elements of the second matrix
    printf("Enter elements of the second matrix:\n");
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < p; j++) {
            printf("Element [%d][%d]: ", i, j);
            scanf("%d", &matrix2[i][j]);
        }
    }

    // Initialize the result matrix with zeros
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < p; j++) {
            result[i][j] = 0;
        }
    }

    // Perform matrix multiplication
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < p; j++) {
            for (int k = 0; k < n; k++) {
                result[i][j] += matrix1[i][k] * matrix2[k][j];
            }
        }
    }

    // Print the resulting matrix
    printf("Resultant matrix after multiplication:\n");
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < p; j++) {
            printf("%d ", result[i][j]);
        }
        printf("\n");
    }

    return 0;
}

Output

Enter the number of rows and columns of the first matrix (m n) -
3
3
Enter the number of columns of the second matrix: 3
Enter elements of the first matrix:
Element [0][0]: 1
Element [0][1]: 2
Element [0][2]: 3
Element [1][0]: 4
Element [1][1]: 5
Element [1][2]: 6
Element [2][0]: 7
Element [2][1]: 8
Element [2][2]: 9
Enter elements of the second matrix:
Element [0][0]: 9
Element [0][1]: 8
Element [0][2]: 7
Element [1][0]: 6
Element [1][1]: 5
Element [1][2]: 4
Element [2][0]: 3
Element [2][1]: 2
Element [2][2]: 1
Resultant matrix after multiplication:
30 24 18
84 69 54
138 114 90

Explanation

1. Input the Dimensions: The program prompts the user to input the dimensions of the matrices. Matrix A has dimensions m x n and matrix B has dimensions n x p.
2. Input the Elements: The user inputs the elements of matrices A and B.
3. Initialize the Result Matrix: The result matrix C is initialized with zeros to store the products.
4. Perform the Multiplication:
   • Three nested loops iterate over the rows of A, the columns of B, and the shared dimension n.
   • Each element of the result matrix is computed as the sum of the products of corresponding elements from A and B.
5. Print the Result: The program prints the elements of the result matrix.