Nearest smaller to right
Write a program to find the nearest smaller element or next smaller element to the right of each element in an array.
Problem
In case of this problem, an array is given and we have to find first smaller element to the right of current element. Similalrly, find the smaller elements for each element in the array and if greater element is not available then return a default value based on the problem.

Example -
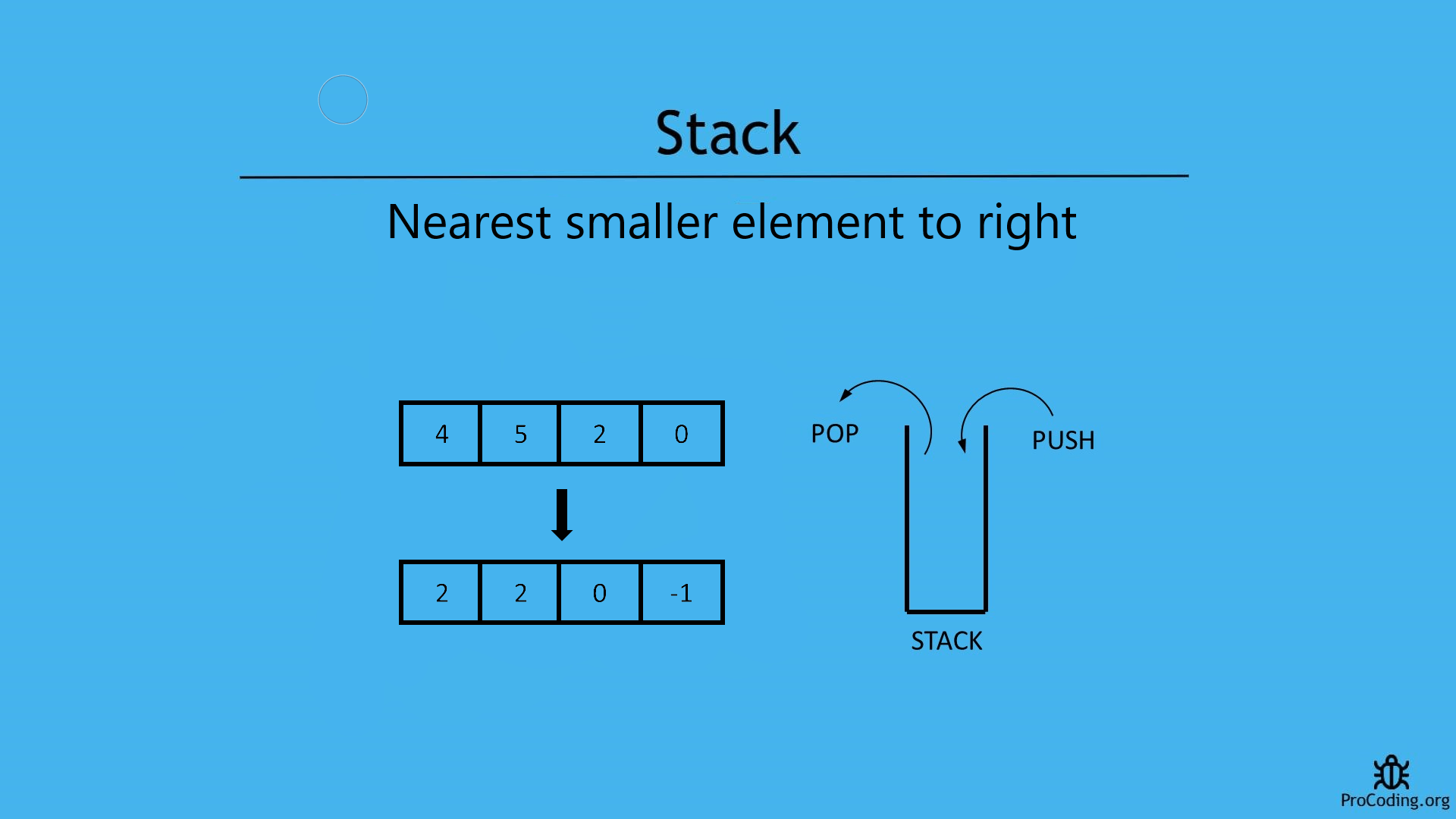
Input: [4, 5, 2, 0]
Output: [2, 2, 0, 1]
Input: [1, 6, 4, 10, 2, 5]
Output: [-1, 4, 2, 2, -1, -1]
Few points to consider:
- If the array is sorted in increasing order, next smaller element will always be -1.
- For the right most element, right smaller element will always be -1.
We will see two ways to solve the problems
Brute-force approach (using nested loops)
In this approach we will use two loops. Outer loop will iterate over all the array items and inner loop will iterate over all the next elements of currently pointed by outer loop. Inner loop will check, if any smaller element will be found then loop will be terminated and if smaller element is not found then -1 will be added as result.
Python
def nearest_smaller_to_right(arr):
result = []
for i in range(0, len(arr)):
for j in range(i+1, len(arr)):
if arr[i] > arr[j]:
result.append(arr[j])
break
else:
result.append(-1)
return result
arr = [6, 4, 10, 2, 5]
print(nearest_smaller_to_right(arr))
JavaScript
function nearestSmallerToRight(arr) {
result = [];
for (let i = 0; i < arr.length; i++) {
let flag = false;
for (let j = i+1; j < arr.length; j++) {
if (arr[i] > arr[j]) {
result.push(arr[j]);
flag = true;
break;
}
}
if (!flag)
result.push(-1);
}
return result;
}
const arr = [6, 4, 10, 2, 5];
console.log(nearestSmallerToRight(arr));
Output
[4, 2, 2, -1, -1]
Although, we have solved this problem using loops but this is not an optimized solution.
Because time complexity of this solution is O(n^2).
Using stack
Algorithm
NearestSmallerToRight(A)
1. for i = A.length to 0
2. if stack is empty
3. result.add(-1)
4. stack.push(A[i])
5. else if stack is not empty
6. while (stack is not empty AND A[i] < top of stack)
7. stack.pop()
8. if stack is empty
9. result.add(-1)
10. else
11. result.add(top of stack)
12. stack.push(A[i])
13. return reverse of result
In this approach, we are using a stack.
We have to start traversing elements of the given array from the end i.e., rightmost element and we will be putting the smallest element in the stack and whenever we get another smaller element then pop the stack and push the new element. Basically, we will be using a stack to keep values available to the right side and which are the smaller ones.
If the stack is empty the smaller element to right will be -1 otherwise top of stack will be the smaller element. At the end we have to reverse the result array because we are working on the input array from the opposite side.
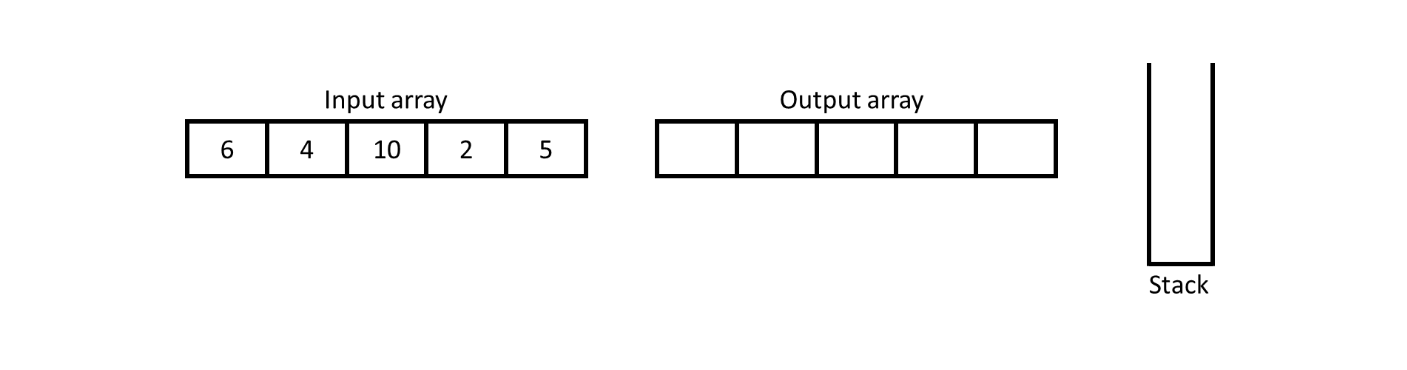
Initially, input array will be given and an output array with stack will be created.
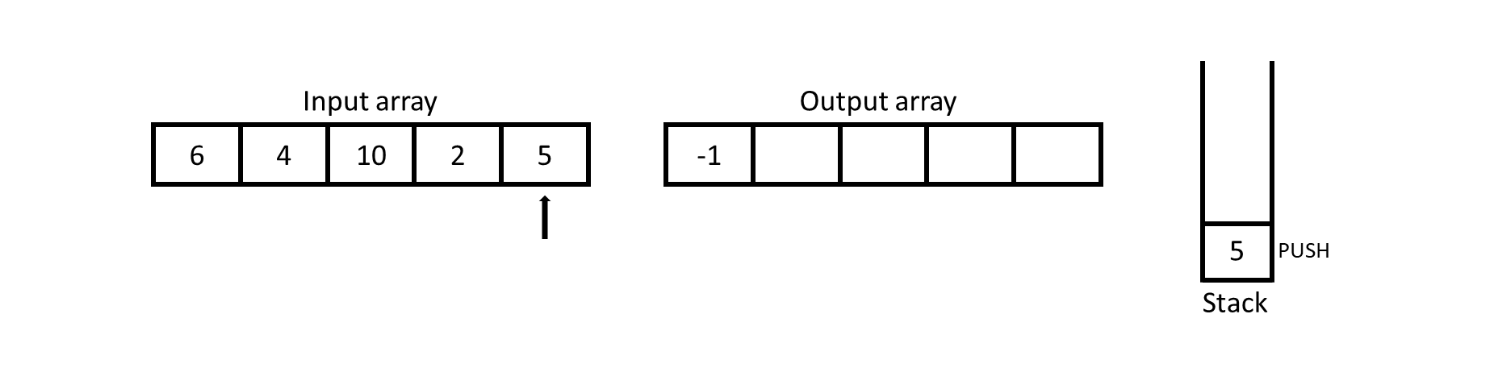
Start traversing of array from the right side and for the rightmost element nearest smaller to right will be -1 and put the value from the input array into the stack for further comparision.
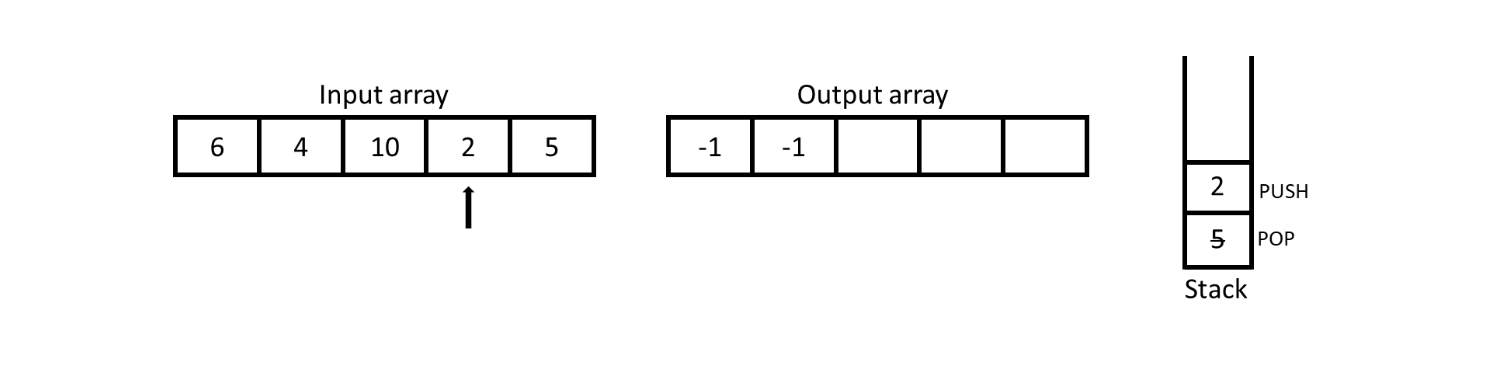
For 2, stack is not empty so we have to check the top most value if it is smaller than 2 or not. Here we observe that 5 (top of stack) is not smaller than 2 so -1 will be inserted into output array and 2 will be pushed into the stack.
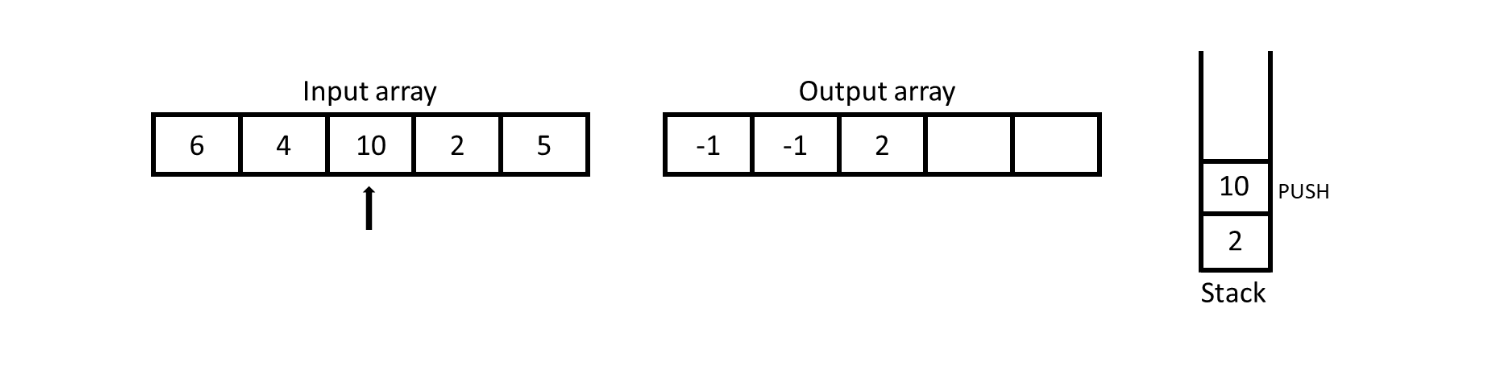
For 10, stack is not empty so check the top of stack and the top of stack i.e., 2 is smaller than 10 so add 2 in the output array and push 10 into the stack.
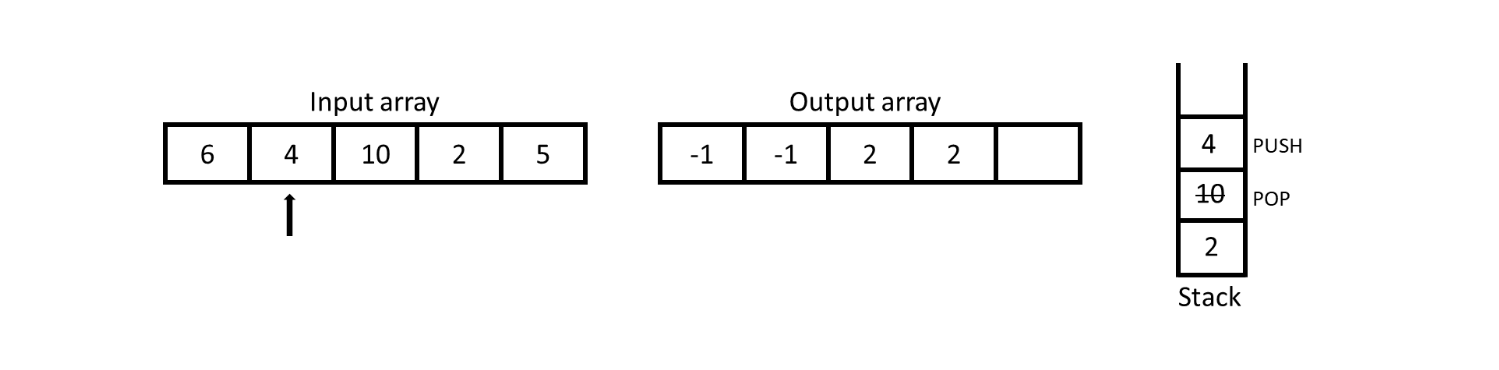
For 4, the top of stack is 10 which is not smaller than 4 so pop off 10 and then the top of stack is 2 which is smaller than 4 so add 2 in the output array and push 4 into the top of stack.
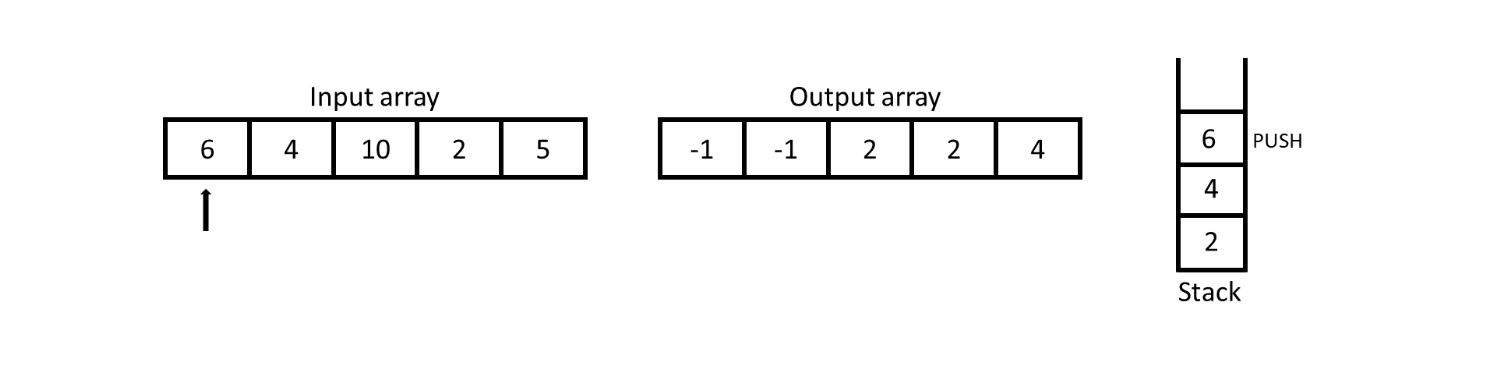
For 6, the top of stack is 4 which is obviously smaller than 6 so insert 6 into the output array and push 6 into the stack.
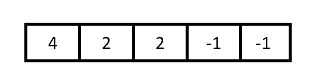
At the end, reverse the output array because we have started the traversal of array from right end and this will be the result.
Program
Python
class Stack:
def __init__(self):
self.stack = []
def isEmpty(self):
return len(self.stack) == 0
def push(self, num):
self.stack.append(num)
def pop(self):
if self.isEmpty():
raise Exception('Stack Underflow')
return self.stack.pop()
def peek(self):
if self.isEmpty():
return None
return self.stack[-1]
def nearest_smaller_to_right(arr):
stack = Stack()
result = []
for i in range(len(arr)-1, -1, -1):
if stack.isEmpty():
result.append(-1)
stack.push(arr[i])
elif not stack.isEmpty():
while(not stack.isEmpty() and arr[i] < stack.peek()):
stack.pop()
if stack.isEmpty():
result.append(-1)
else:
result.append(stack.peek())
stack.push(arr[i])
result.reverse()
return result
arr = [6, 4, 10, 2, 5]
print(nearest_smaller_to_right(arr))
JavaScript
class Stack {
constructor() {
this.stack = [];
}
isEmpty() {
return this.stack.length === 0;
}
push(num) {
this.stack.push(num);
}
pop() {
if (this.isEmpty())
throw 'Stack Underflow';
return this.stack.pop();
}
peek() {
if (this.isEmpty())
throw null;
return this.stack[this.stack.length-1]
}
}
function nearestSmallerToRight(arr) {
const stack = new Stack();
result = [];
for (let i = arr.length-1; i >= 0; i--) {
if (stack.isEmpty()) {
result.push(-1);
stack.push(arr[i]);
}
else if (!stack.isEmpty()) {
while (!stack.isEmpty() && arr[i] < stack.peek()) {
stack.pop();
}
if (stack.isEmpty()) {
result.push(-1);
} else {
result.push(stack.peek());
}
stack.push(arr[i]);
}
}
result.reverse();
return result;
}
const arr = [6, 4, 10, 2, 5];
console.log(nearestSmallerToRight(arr));
Output
[4, 2, 2, -1, -1]