Heap sort

Master Heapsort with this concise guide, covering its O(n log n) time complexity and step-by-step implementation in Python, Java, C++, Go, and Rust. Perfect for developers seeking a deep understanding of Heapsort across multiple languages.

Heapsort

Since we know about Heap and Heapify now, we can easily get the minimum (using min-heap) and maximum (using max-heap). So, if we have an array then we can pull the minimum data and keep inserting it in another array and continuously heapify down (percolate down) to maintain the heap property then we can get a sorted array in another array.

The time complexity of this solution will be O(n log n) because each heapify down operation will take log n time and we will do this for n times which is the same as other sorting algorithms.

But we are using extra space in the form of another array to keep a sorted array. So the space complexity will be O(n).

We can remove the extra space used and do the sorting in place which will be a proper heapsort.

Introduction to Heapsort

Heapsort is an efficient, in-place sorting algorithm that leverages the properties of binary heaps. It can be used to sort an array of elements in either ascending or descending order, depending on whether a min-heap or a max-heap is used. Heapsort is not a stable sort, meaning it does not preserve the relative order of equal elements. However, it has a consistent time complexity of O(nlogn) for all cases.

As we discussed earlier we know the sorting using heap. We aim to reduce the extra space used and put the changes in place. Instead of putting the sorted elements in a separate array, we will maintain the partition in the same array to identify the sorted part and continuously apply heapify algo on the rest of the unsorted part to get max and put it into the end after each iteration.

Heapsort Algorithm

Heapsort uses a max-heap to sort an array in ascending order or a min-heap for descending order. The algorithm consists of two main phases:

Build the Heap: Convert the array into a heap. In a max-heap, the largest element will be at the root.
Sort the Array: Repeatedly extract the root (the largest element in the case of a max-heap), swap it with the last element, reduce the heap size, and heapify the root to maintain the heap property.

Step-by-Step Process

Heapify the Array: Start by building a max-heap from the array. This is done by applying the heapify operation to each non-leaf node, starting from the last non-leaf node up to the root.
Sort the Array: After building the heap, the largest element is at the root. Swap it with the last element of the array and reduce the size of the heap by one. Then, heapify the root again to ensure the max-heap property is maintained. Repeat this process until the heap size is reduced to one.

Let's take the example of this array and sort the elements using heapsort

Heapsort step 1

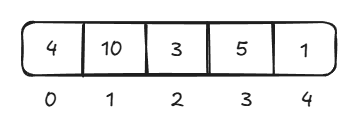
On applying max-heapify, we will get elements in ascending order; if we apply min-heapify, we will get elements in descending order. We will apply max-heapify to get elements in ascending order.

The first step is to apply max-heapify operation on the whole array i.e., from n/2 to 0 to heapify the array and get the highest element at the 0th index. After this the array will get the heap structures.

Once we get the highest element on the 0th index, then swap it with the elemental at last index. We will be maintaining the sorted elements at the end. And heap area is from index 0 to 3.

Heapsort step 2

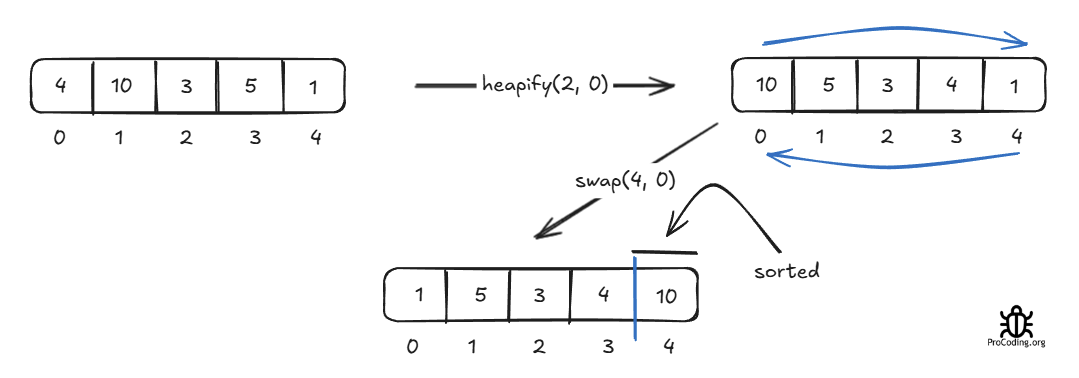
Now the last index is sorted. From this step, we will heapify the element at the 0th index only to get the maximum element at the 0th index and swap it with the last index based on the partition of the sorted array we are maintaining. After each step, we are sure that the element at the 0th index is only disturbed that's why will just heapify that element and we will get the next maximum on the 0th index.

Heapsort step 3

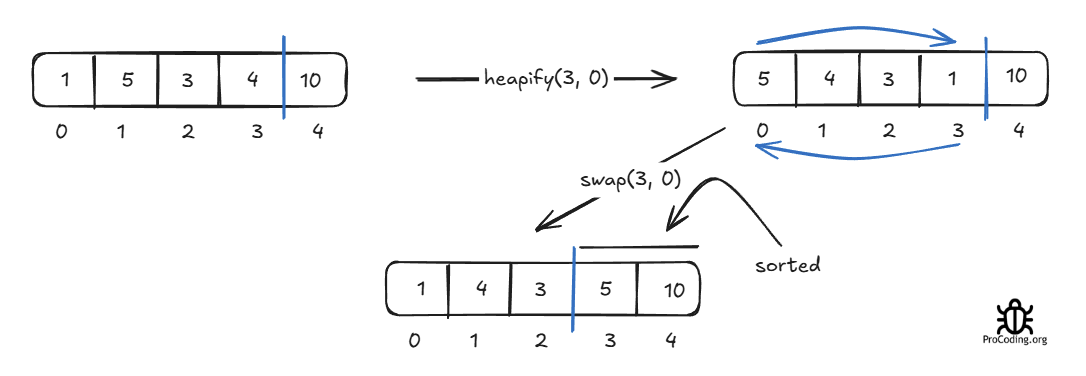
Now elements from 3 to 4 are sorted and we will just focus on elements from 0 to 2. Apply heapify on the 0th index again to get maximum.

Heapsort step 4

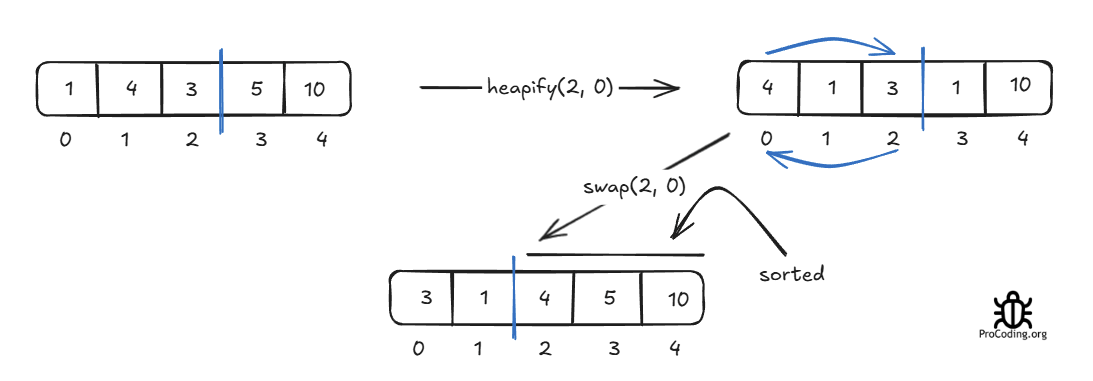
Now elements from index 2 to 4 are sorted. Our focus will be on 0 to 1.

Heapsort step 5

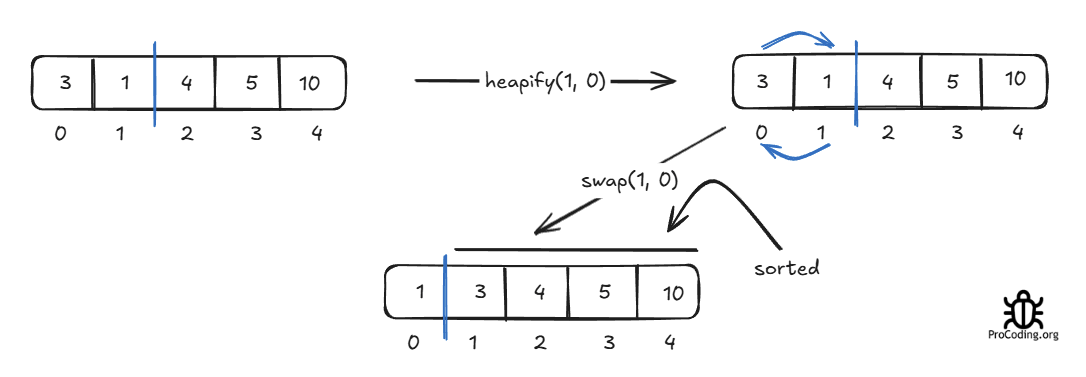
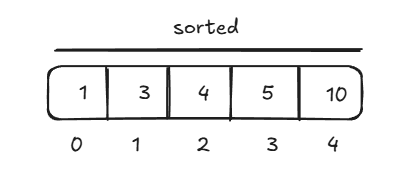
After this step elements from 1 to 4 are sorted and we only only have one element left at the 0th index which is sorted itself. So, we have a final sorted array.

Heapsort step 6

Heapsort Implementation

Python

def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[i] < arr[left]:
        largest = left

    if right < n and arr[largest] < arr[right]:
        largest = right

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heapsort(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

arr = [4, 10, 3, 5, 1]
heapsort(arr)
print(arr)

JavaScript

function heapify(arr, n, i) {
    let largest = i;
    const left = 2 * i + 1;
    const right = 2 * i + 2;

    if (left < n && arr[i] < arr[left]) {
        largest = left;
    }

    if (right < n && arr[largest] < arr[right]) {
        largest = right;
    }

    if (largest !== i) {
        [arr[i], arr[largest]] = [arr[largest], arr[i]];  // Swap
        heapify(arr, n, largest);
    }
}

function heapsort(arr) {
    const n = arr.length;

    // Build heap (rearrange array)
    for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // One by one extract an element from heap
    for (let i = n - 1; i > 0; i--) {
        [arr[0], arr[i]] = [arr[i], arr[0]];  // Move current root to end
        heapify(arr, i, 0);
    }
}

const arr = [4, 10, 3, 5, 1];
heapsort(arr);
console.log(arr);

Java

public class HeapSort {

    public void heapify(int[] arr, int n, int i) {
        int largest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;

        if (left < n && arr[i] < arr[left]) {
            largest = left;
        }

        if (right < n && arr[largest] < arr[right]) {
            largest = right;
        }

        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;

            heapify(arr, n, largest);
        }
    }

    public void heapsort(int[] arr) {
        int n = arr.length;

        // Build heap (rearrange array)
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }

        // One by one extract an element from heap
        for (int i = n - 1; i > 0; i--) {
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            heapify(arr, i, 0);
        }
    }

    public static void main(String[] args) {
        int[] arr = {4, 10, 3, 5, 1};
        HeapSort sorter = new HeapSort();
        sorter.heapsort(arr);
        
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

C++

#include <iostream>
#include <vector>

using namespace std;

void heapify(vector<int>& arr, int n, int i) {
    int largest = i;         // Initialize largest as root
    int left = 2 * i + 1;    // left = 2*i + 1
    int right = 2 * i + 2;   // right = 2*i + 2

    // If left child is larger than root
    if (left < n && arr[left] > arr[largest])
        largest = left;

    // If right child is larger than largest so far
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // If largest is not root
    if (largest != i) {
        swap(arr[i], arr[largest]);

        // Recursively heapify the affected sub-tree
        heapify(arr, n, largest);
    }
}

void heapsort(vector<int>& arr) {
    int n = arr.size();

    // Build heap (rearrange array)
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);

    // One by one extract an element from heap
    for (int i = n - 1; i > 0; i--) {
        // Move current root to end
        swap(arr[0], arr[i]);

        // Call max heapify on the reduced heap
        heapify(arr, i, 0);
    }
}

int main() {
    vector<int> arr = {4, 10, 3, 5, 1};
    heapsort(arr);
    for (int i = 0; i < arr.size(); i++)
        cout << arr[i] << " ";
    cout << endl;
    return 0;
}

package main

import "fmt"

func heapify(arr []int, n, i int) {
	largest := i
	left := 2*i + 1
	right := 2*i + 2

	if left < n && arr[i] < arr[left] {
		largest = left
	}

	if right < n && arr[largest] < arr[right] {
		largest = right
	}

	if largest != i {
		arr[i], arr[largest] = arr[largest], arr[i]
		heapify(arr, n, largest)
	}
}

func heapsort(arr []int) {
	n := len(arr)

	// Build heap (rearrange array)
	for i := n/2 - 1; i >= 0; i-- {
		heapify(arr, n, i)
	}

	// One by one extract an element from heap
	for i := n - 1; i > 0; i-- {
		arr[0], arr[i] = arr[i], arr[0]
		heapify(arr, i, 0)
	}
}

func main() {
	arr := []int{4, 10, 3, 5, 1}
	heapsort(arr)
	fmt.Println(arr)
}

Rust

fn heapify(arr: &mut [i32], n: usize, i: usize) {
    let mut largest = i;
    let left = 2 * i + 1;
    let right = 2 * i + 2;

    if left < n && arr[left] > arr[largest] {
        largest = left;
    }

    if right < n && arr[right] > arr[largest] {
        largest = right;
    }

    if largest != i {
        arr.swap(i, largest);
        heapify(arr, n, largest);
    }
}

fn heapsort(arr: &mut [i32]) {
    let n = arr.len();

    // Build heap (rearrange array)
    for i in (0..n / 2).rev() {
        heapify(arr, n, i);
    }

    // One by one extract an element from heap
    for i in (1..n).rev() {
        arr.swap(0, i);
        heapify(arr, i, 0);
    }
}

fn main() {
    let mut arr = [4, 10, 3, 5, 1];

    heapsort(&mut arr);

    println!("Sorted array is: {:?}", arr);
}

Output

[1, 3, 4, 5, 10]

Heapsort Time Complexity

Heapsort has a time complexity of O(n log n) for the following reasons:

Heap Building: The initial heap construction takes O(n) time.
Heapify Operation: After extracting the root, reheapification (heapify) takes O(log n) time. Since we do this for n elements, the sorting phase takes O(n log n).