Max heap
Discover the essentials of Max Heap data structures. Explore how Max Heaps work, their key properties, and learn how to perform operations like insertion, deletion, and heapify with step-by-step examples.
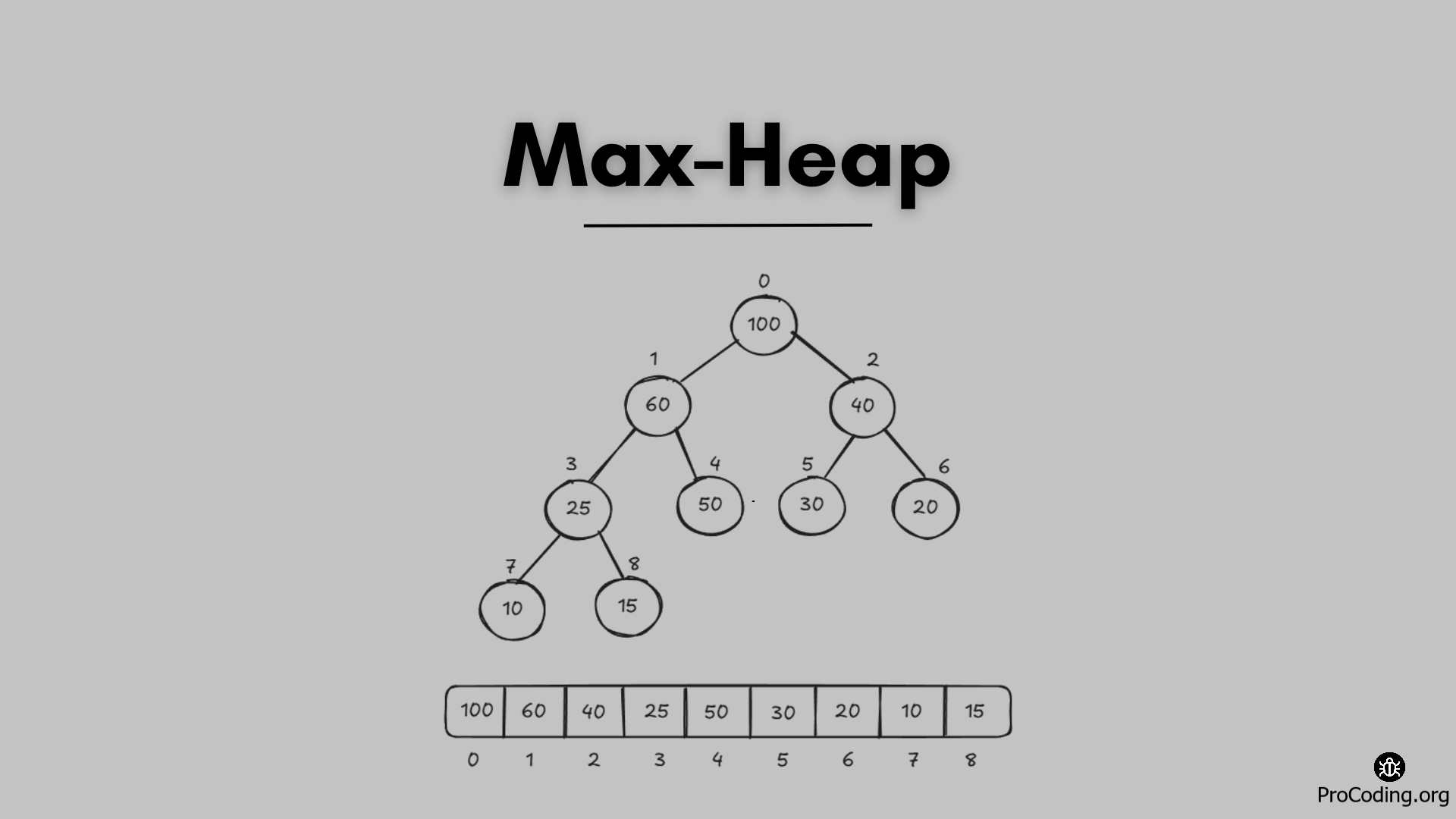
Table of contents
- Insertion in max-heap
- Remove element from the max heap
- Max heap implementation - Recursive
- Max heap implementation - Iterative
A Max-heap is a data structure in which each node is greater than its children. It is a tree-based data structure but implemented as an array.
Max-heaps are commonly used for sorting.
Heap always maintains the heap property. For max-heap heap property will be -
Maintaining heap property (for max-heap) means comparing the left child and right child with the root and among all three, the maximum will become the root.

To understand about heap please refer to this article -
Insertion in max-heap
While insertion we have to maintain the heap properties -
- Complete binary tree
- Max heap order
Insertion
Take the example of this heap and try to insert a new node -
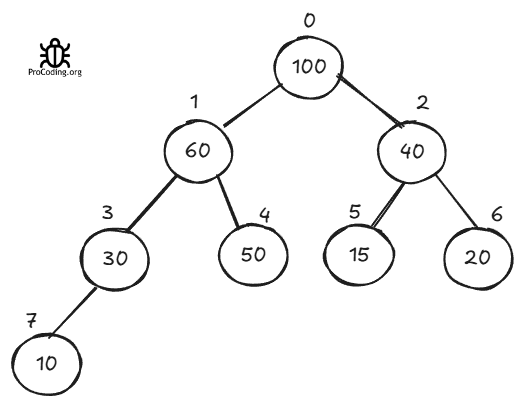
Its representation in the form of an array will be like this -
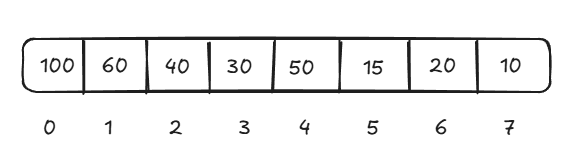
Let's insert 70 into this heap
For insertion, add the new element at the end of the array i.e., insert the new element as a leaf node then move the element to its correct position. The correct position is actually where this node will be higher than its children and lower than its parent.
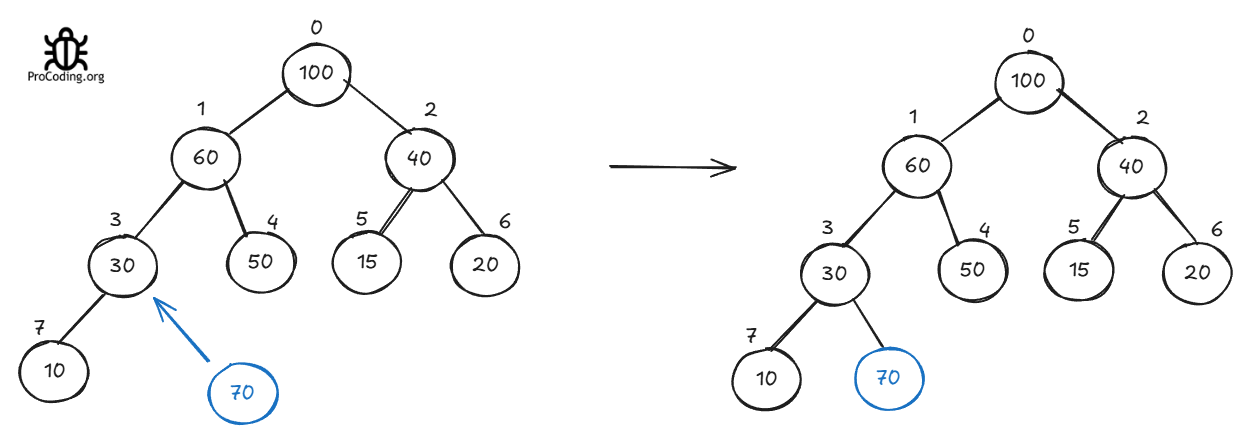
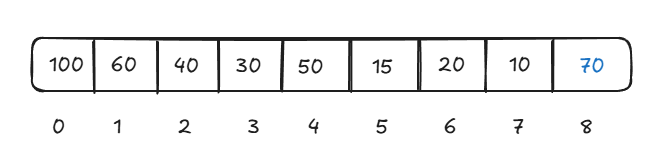
We will do this by comparing this new element to its parent at each step and moving this new upwards until it is higher than its parent.
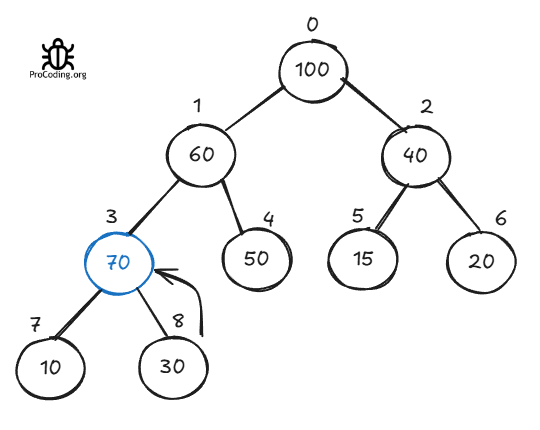
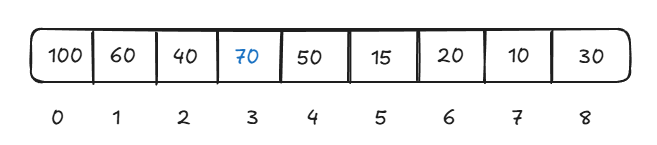
Do the same steps again. Compare 70 to its new parent and move this to its correct position.
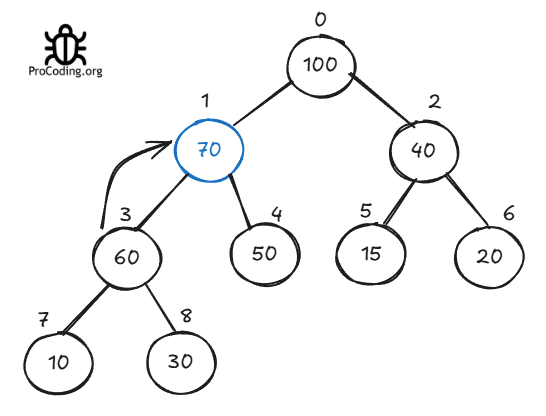
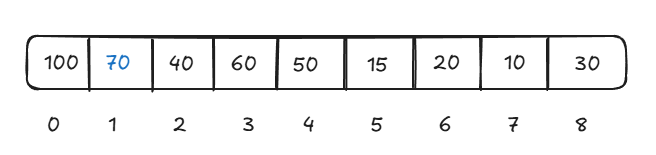
Now 70 is inserted at its correct position.
The time complexity to insert a new element in a heap will be O(h) where h is the height of the tree. The height of a balanced binary tree is log n so the insertion of a new element will take O(log n) time which is better than what we were getting in the case of the Binary tree implementation of heap. That's why it's better to store data in the form of an array for a heap.
The process of moving data up is called percolate up or bubble up or heapify up or sift up.
Remove element from the max heap
This is the main operation of the heap. All the elements will be removed from the 0th index always because the maximum element will always be at index 0. Since we are storing data in such a way.
This is the main purpose of a max heap i.e., whatever data we are storing in the heap we are always sure that while removing the data we will be getting is maximum among all the data stored.
We can say that the maximum element has the highest priority and it will picked up at a given time.
Deletion
Let's try to remove an element from the heap that we created earlier. So, 100 will be removed from the heap since this is the root of max-heap.
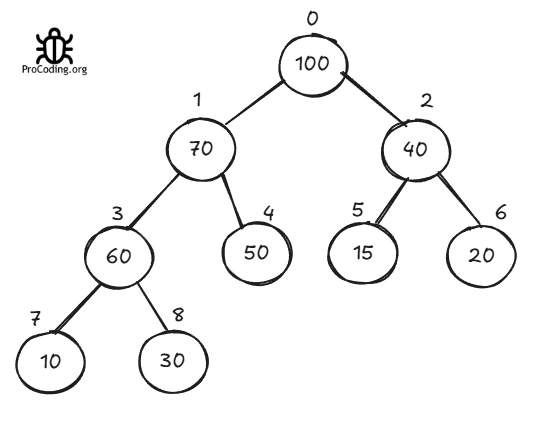
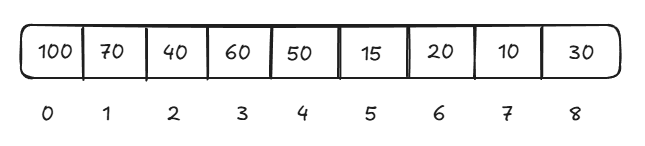
But if we will remove the root element then the heap will be disturbed and we will have to do some extra operations. So rather than removing the element directly from the root, replace it with the last element from heap and the replace the last element.
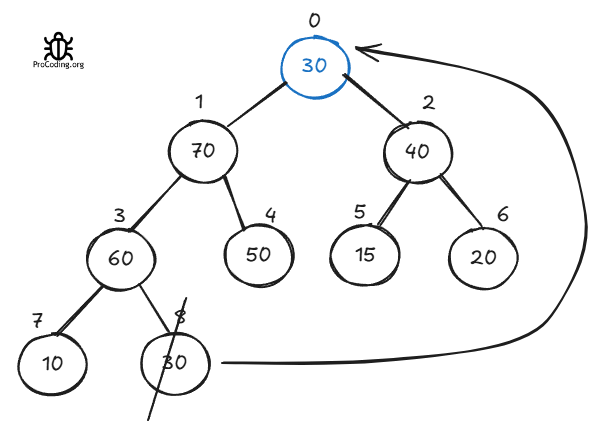
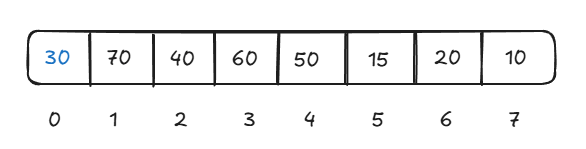
Now the root element is removed from the heap but the heap property is disturbed i.e., not all the root elements are greater than their children.
But that's not a big deal we already know we can do that by just iterating over all the elements comparing the root elements with children and moving the higher element upwards as a root. But this time start with the root element because we know this element is the reason for the disturbance of heap property.
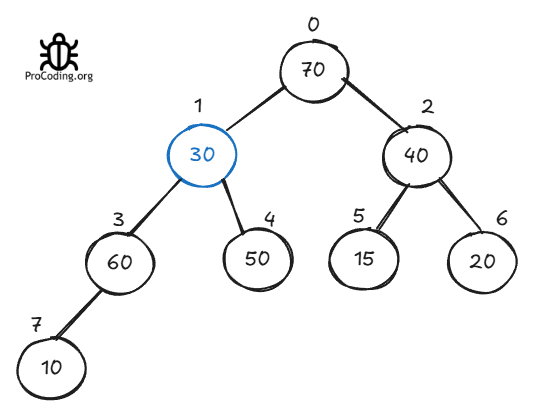
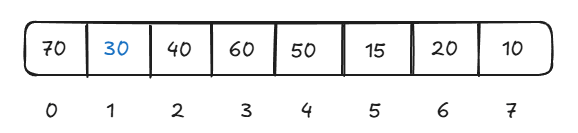
Again let's see if 30 is still smaller than its children then move this downwards.
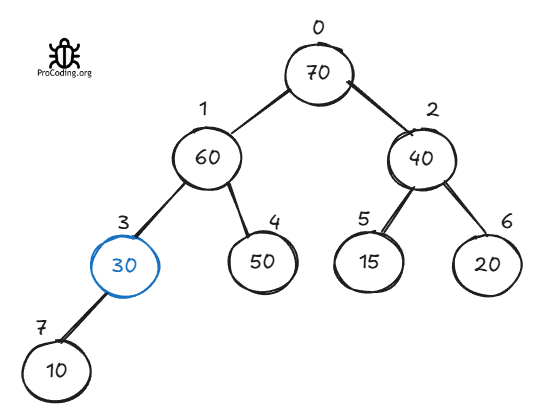
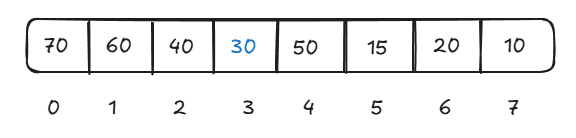
This is the final heap after removing an element. Time complexity will be O(log n) for removing an element.
The process of moving data down is called percolate down or **bubble down or heapify down or sift down.
Max heap implementation - Recursive
Here, we will implement percolate functionality in recursive way.
Python
class MaxHeap:
def __init__(self):
# Initialize an empty list to store the heap elements
self.heap = []
def is_empty(self):
# Check if the heap is empty
return len(self.heap) == 0
def get_max(self):
# Return the maximum element without removing it
if self.is_empty():
return None
return self.heap[0]
def get_size(self):
# Return the size of the heap
return len(self.heap)
def insert(self, value):
# Insert the value into the heap
self.heap.append(value)
self._percolate_up(len(self.heap) - 1)
def _percolate_up(self, index):
# Move the element at the given index up the heap to maintain the heap property
parent_index = (index - 1) // 2
if index > 0 and self.heap[index] > self.heap[parent_index]:
# Swap the current element with its parent if it's greater
self.heap[index], self.heap[parent_index] = (
self.heap[parent_index],
self.heap[index],
)
self._percolate_up(parent_index)
def remove(self):
# Remove and return the maximum element from the heap (root of the heap)
if self.is_empty():
return None
if len(self.heap) == 1:
return self.heap.pop()
root = self.heap[0]
# Move the last element to the root and percolate down
self.heap[0] = self.heap.pop()
self._percolate_down(0)
return root
def _percolate_down(self, index):
# Move the element at the given index down the heap to maintain the heap property
size = len(self.heap)
largest = index
left = 2 * index + 1
right = 2 * index + 2
# Check if the left child exists and is greater than the current element
if left < size and self.heap[left] > self.heap[largest]:
largest = left
# Check if the right child exists and is greater than the current largest
if right < size and self.heap[right] > self.heap[largest]:
largest = right
# If the largest element is not the current element, swap and continue percolating down
if largest != index:
self.heap[index], self.heap[largest] = self.heap[largest], self.heap[index]
self._percolate_down(largest)
max_heap = MaxHeap()
max_heap.insert(10)
max_heap.insert(4)
max_heap.insert(9)
max_heap.insert(2)
max_heap.insert(7)
print("Max element peek:", max_heap.get_max()) # Output: 10
print("Max element:", max_heap.remove()) # Output: 10
print("Max element:", max_heap.remove()) # Output: 9
max_heap.insert(5)
print("Max element:", max_heap.remove()) # Output: 7
JavaScript
class MaxHeap {
constructor() {
this.heap = [];
}
isEmpty() {
return this.heap.length === 0;
}
getMax() {
if (this.isEmpty()) {
return null;
}
return this.heap[0];
}
getSize() {
return this.heap.length;
}
insert(value) {
this.heap.push(value);
this.percolateUp(this.heap.length - 1);
}
percolateUp(index) {
const parentIndex = Math.floor((index - 1) / 2);
if (index > 0 && this.heap[index] > this.heap[parentIndex]) {
[this.heap[index], this.heap[parentIndex]] = [this.heap[parentIndex], this.heap[index]];
this.percolateUp(parentIndex);
}
}
remove() {
if (this.isEmpty()) {
return null;
}
if (this.heap.length === 1) {
return this.heap.pop();
}
const root = this.heap[0];
this.heap[0] = this.heap.pop();
this.percolateDown(0);
return root;
}
percolateDown(index) {
const size = this.heap.length;
let largest = index;
const left = 2 * index + 1;
const right = 2 * index + 2;
if (left < size && this.heap[left] > this.heap[largest]) {
largest = left;
}
if (right < size && this.heap[right] > this.heap[largest]) {
largest = right;
}
if (largest !== index) {
[this.heap[index], this.heap[largest]] = [this.heap[largest], this.heap[index]];
this.percolateDown(largest);
}
}
}
// Example usage
const maxHeap = new MaxHeap();
maxHeap.insert(10);
maxHeap.insert(4);
maxHeap.insert(9);
maxHeap.insert(2);
maxHeap.insert(7);
console.log("Max element peek:", maxHeap.getMax()); // Output: 10
console.log("Max element:", maxHeap.remove()); // Output: 10
console.log("Max element:", maxHeap.remove()); // Output: 9
maxHeap.insert(5);
console.log("Max element:", maxHeap.remove()); // Output: 7
Java
import java.util.ArrayList;
import java.util.List;
public class MaxHeap {
private List<Integer> heap;
public MaxHeap() {
heap = new ArrayList<>();
}
public boolean isEmpty() {
return heap.isEmpty();
}
public Integer getMax() {
if (isEmpty()) {
return null;
}
return heap.get(0);
}
public int getSize() {
return heap.size();
}
public void insert(int value) {
heap.add(value);
percolateUp(heap.size() - 1);
}
private void percolateUp(int index) {
int parentIndex = (index - 1) / 2;
if (index > 0 && heap.get(index) > heap.get(parentIndex)) {
swap(index, parentIndex);
percolateUp(parentIndex);
}
}
public Integer remove() {
if (isEmpty()) {
return null;
}
if (heap.size() == 1) {
return heap.remove(heap.size() - 1);
}
int root = heap.get(0);
heap.set(0, heap.remove(heap.size() - 1));
percolateDown(0);
return root;
}
private void percolateDown(int index) {
int size = heap.size();
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < size && heap.get(left) > heap.get(largest)) {
largest = left;
}
if (right < size && heap.get(right) > heap.get(largest)) {
largest = right;
}
if (largest != index) {
swap(index, largest);
percolateDown(largest);
}
}
private void swap(int i, int j) {
int temp = heap.get(i);
heap.set(i, heap.get(j));
heap.set(j, temp);
}
public static void main(String[] args) {
MaxHeap maxHeap = new MaxHeap();
maxHeap.insert(10);
maxHeap.insert(4);
maxHeap.insert(9);
maxHeap.insert(2);
maxHeap.insert(7);
System.out.println("Max element peek: " + maxHeap.getMax()); // Output: 10
System.out.println("Max element: " + maxHeap.remove()); // Output: 10
System.out.println("Max element: " + maxHeap.remove()); // Output: 9
maxHeap.insert(5);
System.out.println("Max element: " + maxHeap.remove()); // Output: 7
}
}
Go
package main
import (
"fmt"
)
type MaxHeap struct {
heap []int
}
func NewMaxHeap() *MaxHeap {
return &MaxHeap{heap: []int{}}
}
func (h *MaxHeap) IsEmpty() bool {
return len(h.heap) == 0
}
func (h *MaxHeap) GetMax() int {
if h.IsEmpty() {
return -1 // or some other indicator of empty heap
}
return h.heap[0]
}
func (h *MaxHeap) GetSize() int {
return len(h.heap)
}
func (h *MaxHeap) Insert(value int) {
h.heap = append(h.heap, value)
h.percolateUp(len(h.heap) - 1)
}
func (h *MaxHeap) percolateUp(index int) {
if index <= 0 {
return
}
parentIndex := (index - 1) / 2
if h.heap[index] > h.heap[parentIndex] {
h.heap[index], h.heap[parentIndex] = h.heap[parentIndex], h.heap[index]
h.percolateUp(parentIndex) // Recursive call
}
}
func (h *MaxHeap) Remove() int {
if h.IsEmpty() {
return -1 // or some other indicator of empty heap
}
if len(h.heap) == 1 {
root := h.heap[0]
h.heap = h.heap[:0]
return root
}
root := h.heap[0]
h.heap[0] = h.heap[len(h.heap)-1]
h.heap = h.heap[:len(h.heap)-1]
h.percolateDown(0)
return root
}
func (h *MaxHeap) percolateDown(index int) {
size := len(h.heap)
largest := index
left := 2*index + 1
right := 2*index + 2
if left < size && h.heap[left] > h.heap[largest] {
largest = left
}
if right < size && h.heap[right] > h.heap[largest] {
largest = right
}
if largest != index {
h.heap[index], h.heap[largest] = h.heap[largest], h.heap[index]
h.percolateDown(largest)
}
}
func main() {
maxHeap := NewMaxHeap()
maxHeap.Insert(10)
maxHeap.Insert(4)
maxHeap.Insert(9)
maxHeap.Insert(2)
maxHeap.Insert(7)
fmt.Println("Max element peek:", maxHeap.GetMax()) // Output: 10
fmt.Println("Max element:", maxHeap.Remove()) // Output: 10
fmt.Println("Max element:", maxHeap.Remove()) // Output: 9
maxHeap.Insert(5)
fmt.Println("Max element:", maxHeap.Remove()) // Output: 7
}
C++
#include <iostream>
#include <vector>
class MaxHeap {
private:
std::vector<int> heap;
void percolateUp(int index) {
// Base case: if index is 0, there's no parent to compare with
if (index <= 0) {
return;
}
int parentIndex = (index - 1) / 2;
// If the current element is greater than its parent, swap and continue
if (heap[index] > heap[parentIndex]) {
std::swap(heap[index], heap[parentIndex]);
percolateUp(parentIndex); // Recursive call
}
}
void percolateDown(int index) {
int size = heap.size();
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < size && heap[left] > heap[largest]) {
largest = left;
}
if (right < size && heap[right] > heap[largest]) {
largest = right;
}
if (largest != index) {
std::swap(heap[index], heap[largest]);
percolateDown(largest);
}
}
public:
MaxHeap() = default;
bool isEmpty() const {
return heap.empty();
}
int getMax() const {
if (isEmpty()) {
return -1; // or some other indicator of empty heap
}
return heap[0];
}
int getSize() const {
return heap.size();
}
void insert(int value) {
heap.push_back(value);
percolateUp(heap.size() - 1);
}
int remove() {
if (isEmpty()) {
return -1; // or some other indicator of empty heap
}
if (heap.size() == 1) {
int root = heap[0];
heap.pop_back();
return root;
}
int root = heap[0];
heap[0] = heap.back();
heap.pop_back();
percolateDown(0);
return root;
}
};
int main() {
MaxHeap maxHeap;
maxHeap.insert(10);
maxHeap.insert(4);
maxHeap.insert(9);
maxHeap.insert(2);
maxHeap.insert(7);
std::cout << "Max element peek: " << maxHeap.getMax() << std::endl; // Output: 10
std::cout << "Max element: " << maxHeap.remove() << std::endl; // Output: 10
std::cout << "Max element: " << maxHeap.remove() << std::endl; // Output: 9
maxHeap.insert(5);
std::cout << "Max element: " << maxHeap.remove() << std::endl; // Output: 7
return 0;
}
Rust
struct MaxHeap {
heap: Vec<i32>,
}
impl MaxHeap {
fn new() -> Self {
MaxHeap { heap: Vec::new() }
}
fn is_empty(&self) -> bool {
self.heap.is_empty()
}
fn get_max(&self) -> Option<i32> {
if self.is_empty() {
None
} else {
Some(self.heap[0])
}
}
fn get_size(&self) -> usize {
self.heap.len()
}
fn insert(&mut self, value: i32) {
self.heap.push(value);
self.percolate_up(self.get_size() - 1);
}
fn percolate_up(&mut self, index: usize) {
// Base case: if index is 0, there's no parent to compare with
if index == 0 {
return;
}
let parent_index = (index - 1) / 2;
// If the current element is greater than its parent, swap and recurse
if self.heap[index] > self.heap[parent_index] {
self.heap.swap(index, parent_index);
// Recursively call percolate_up with the parent index
self.percolate_up(parent_index);
}
}
fn remove(&mut self) -> Option<i32> {
if self.is_empty() {
return None;
}
if self.get_size() == 1 {
return self.heap.pop();
}
let root = self.heap[0];
self.heap[0] = self.heap.pop().unwrap();
self.percolate_down(0);
Some(root)
}
fn percolate_down(&mut self, index: usize) {
let mut largest = index;
let left = 2 * index + 1;
let right = 2 * index + 2;
let size = self.get_size();
if left < size && self.heap[left] > self.heap[largest] {
largest = left;
}
if right < size && self.heap[right] > self.heap[largest] {
largest = right;
}
if largest != index {
self.heap.swap(index, largest);
self.percolate_down(largest);
}
}
}
fn main() {
let mut max_heap = MaxHeap::new();
max_heap.insert(10);
max_heap.insert(4);
max_heap.insert(9);
max_heap.insert(2);
max_heap.insert(7);
println!("Max element peek: {:?}", max_heap.get_max()); // Output: Some(10)
println!("Max element: {:?}", max_heap.remove()); // Output: Some(10)
println!("Max element: {:?}", max_heap.remove()); // Output: Some(9)
max_heap.insert(5);
println!("Max element: {:?}", max_heap.remove()); // Output: Some(7)
}
Max heap implementation - Iterative
Here, we will implement percolate functionality in iterative way.
Python
class MaxHeap:
def __init__(self):
# Initialize an empty list to store the heap elements
self.heap = []
def is_empty(self):
# Check if the heap is empty
return len(self.heap) == 0
def get_max(self):
# Return the maximum element (the root) without removing it
if self.is_empty():
return None
return self.heap[0]
def get_size(self):
# Return the size of the heap
return len(self.heap)
def insert(self, value):
# Insert a new value into the heap
self.heap.append(value)
self._percolate_up(len(self.heap) - 1)
def _percolate_up(self, index):
# Move the element at the given index up the heap to maintain the heap property
parent_index = (index - 1) // 2
while index > 0 and self.heap[index] > self.heap[parent_index]:
# Swap the current element with its parent if it's larger
self.heap[index], self.heap[parent_index] = (
self.heap[parent_index],
self.heap[index],
)
index = parent_index
parent_index = (index - 1) // 2
def remove(self):
# Remove and return the maximum element (root of the heap)
if self.is_empty():
return None
if len(self.heap) == 1:
return self.heap.pop()
root = self.heap[0]
# Move the last element to the root and percolate down
self.heap[0] = self.heap.pop()
self._percolate_down(0)
return root
def _percolate_down(self, index):
# Move the element at the given index down the heap to maintain the heap property
size = len(self.heap)
largest = index
while True:
left = 2 * largest + 1
right = 2 * largest + 2
if left < size and self.heap[left] > self.heap[largest]:
largest = left
if right < size and self.heap[right] > self.heap[largest]:
largest = right
if largest != index:
self.heap[index], self.heap[largest] = (
self.heap[largest],
self.heap[index],
)
index = largest
else:
break
max_heap = MaxHeap()
max_heap.insert(10)
max_heap.insert(4)
max_heap.insert(9)
max_heap.insert(2)
max_heap.insert(7)
print("Max element peek:", max_heap.get_max()) # Output: 10
print("Max element:", max_heap.remove()) # Output: 10
print("Max element:", max_heap.remove()) # Output: 9
max_heap.insert(5)
print("Max element:", max_heap.remove()) # Output: 7
JavaScript
class MaxHeap {
constructor() {
// Initialize an empty array to store the heap elements
this.heap = [];
}
isEmpty() {
// Check if the heap is empty
return this.heap.length === 0;
}
getMax() {
// Return the maximum element (the root) without removing it
if (this.isEmpty()) {
return null;
}
return this.heap[0];
}
getSize() {
// Return the size of the heap
return this.heap.length;
}
insert(value) {
// Insert a new value into the heap
this.heap.push(value);
this.percolateUp(this.heap.length - 1);
}
percolateUp(index) {
// Move the element at the given index up the heap to maintain the heap property
let parentIndex = Math.floor((index - 1) / 2);
while (index > 0 && this.heap[index] > this.heap[parentIndex]) {
// Swap the current element with its parent if it's larger
[this.heap[index], this.heap[parentIndex]] = [this.heap[parentIndex], this.heap[index]];
index = parentIndex;
parentIndex = Math.floor((index - 1) / 2);
}
}
remove() {
// Remove and return the maximum element (root of the heap)
if (this.isEmpty()) {
return null;
}
if (this.heap.length === 1) {
return this.heap.pop();
}
const root = this.heap[0];
// Move the last element to the root and percolate down
this.heap[0] = this.heap.pop();
this.percolateDown(0);
return root;
}
percolateDown(index) {
// Move the element at the given index down the heap to maintain the heap property
const size = this.heap.length;
let largest = index;
while (true) {
const left = 2 * largest + 1;
const right = 2 * largest + 2;
if (left < size && this.heap[left] > this.heap[largest]) {
largest = left;
}
if (right < size && this.heap[right] > this.heap[largest]) {
largest = right;
}
if (largest !== index) {
[this.heap[index], this.heap[largest]] = [this.heap[largest], this.heap[index]];
index = largest;
} else {
break;
}
}
}
}
// Example usage:
const maxHeap = new MaxHeap();
maxHeap.insert(10);
maxHeap.insert(4);
maxHeap.insert(9);
maxHeap.insert(2);
maxHeap.insert(7);
console.log("Max element peek:", maxHeap.getMax()); // Output: 10
console.log("Max element:", maxHeap.remove()); // Output: 10
console.log("Max element:", maxHeap.remove()); // Output: 9
maxHeap.insert(5);
console.log("Max element:", maxHeap.remove()); // Output: 7
Java
import java.util.ArrayList;
import java.util.List;
class MaxHeap {
private List<Integer> heap;
public MaxHeap() {
// Initialize an empty list to store the heap elements
this.heap = new ArrayList<>();
}
public boolean isEmpty() {
// Check if the heap is empty
return heap.isEmpty();
}
public Integer getMax() {
// Return the maximum element (the root) without removing it
if (isEmpty()) {
return null;
}
return heap.get(0);
}
public int getSize() {
// Return the size of the heap
return heap.size();
}
public void insert(int value) {
// Insert a new value into the heap
heap.add(value);
percolateUp(heap.size() - 1);
}
private void percolateUp(int index) {
// Move the element at the given index up the heap to maintain the heap property
int parentIndex = (index - 1) / 2;
while (index > 0 && heap.get(index) > heap.get(parentIndex)) {
// Swap the current element with its parent if it's larger
swap(index, parentIndex);
index = parentIndex;
parentIndex = (index - 1) / 2;
}
}
public Integer remove() {
// Remove and return the maximum element (root of the heap)
if (isEmpty()) {
return null;
}
if (heap.size() == 1) {
return heap.remove(heap.size() - 1);
}
int root = heap.get(0);
// Move the last element to the root and percolate down
heap.set(0, heap.remove(heap.size() - 1));
percolateDown(0);
return root;
}
private void percolateDown(int index) {
// Move the element at the given index down the heap to maintain the heap property
int size = heap.size();
int largest = index;
while (true) {
int left = 2 * largest + 1;
int right = 2 * largest + 2;
if (left < size && heap.get(left) > heap.get(largest)) {
largest = left;
}
if (right < size && heap.get(right) > heap.get(largest)) {
largest = right;
}
if (largest != index) {
swap(index, largest);
index = largest;
} else {
break;
}
}
}
private void swap(int index1, int index2) {
int temp = heap.get(index1);
heap.set(index1, heap.get(index2));
heap.set(index2, temp);
}
// Example usage:
public static void main(String[] args) {
MaxHeap maxHeap = new MaxHeap();
maxHeap.insert(10);
maxHeap.insert(4);
maxHeap.insert(9);
maxHeap.insert(2);
maxHeap.insert(7);
System.out.println("Max element peek: " + maxHeap.getMax()); // Output: 10
System.out.println("Max element: " + maxHeap.remove()); // Output: 10
System.out.println("Max element: " + maxHeap.remove()); // Output: 9
maxHeap.insert(5);
System.out.println("Max element: " + maxHeap.remove()); // Output: 7
}
}
Go
package main
import "fmt"
type MaxHeap struct {
heap []int
}
func NewMaxHeap() *MaxHeap {
return &MaxHeap{heap: []int{}}
}
func (h *MaxHeap) IsEmpty() bool {
return len(h.heap) == 0
}
func (h *MaxHeap) GetMax() int {
if h.IsEmpty() {
return -1 // Returning -1 for an empty heap, could also return an error
}
return h.heap[0]
}
func (h *MaxHeap) GetSize() int {
return len(h.heap)
}
func (h *MaxHeap) Insert(value int) {
h.heap = append(h.heap, value)
h.percolateUp(len(h.heap) - 1)
}
func (h *MaxHeap) percolateUp(index int) {
parentIndex := (index - 1) / 2
for index > 0 && h.heap[index] > h.heap[parentIndex] {
h.heap[index], h.heap[parentIndex] = h.heap[parentIndex], h.heap[index]
index = parentIndex
parentIndex = (index - 1) / 2
}
}
func (h *MaxHeap) Remove() int {
if h.IsEmpty() {
return -1 // Returning -1 for an empty heap, could also return an error
}
if len(h.heap) == 1 {
return h.heap[0]
}
root := h.heap[0]
h.heap[0] = h.heap[len(h.heap)-1]
h.heap = h.heap[:len(h.heap)-1]
h.percolateDown(0)
return root
}
func (h *MaxHeap) percolateDown(index int) {
size := len(h.heap)
largest := index
for {
left := 2*largest + 1
right := 2*largest + 2
if left < size && h.heap[left] > h.heap[largest] {
largest = left
}
if right < size && h.heap[right] > h.heap[largest] {
largest = right
}
if largest != index {
h.heap[index], h.heap[largest] = h.heap[largest], h.heap[index]
index = largest
} else {
break
}
}
}
func main() {
maxHeap := NewMaxHeap()
maxHeap.Insert(10)
maxHeap.Insert(4)
maxHeap.Insert(9)
maxHeap.Insert(2)
maxHeap.Insert(7)
fmt.Println("Max element peek:", maxHeap.GetMax()) // Output: 10
fmt.Println("Max element:", maxHeap.Remove()) // Output: 10
fmt.Println("Max element:", maxHeap.Remove()) // Output: 9
maxHeap.Insert(5)
fmt.Println("Max element:", maxHeap.Remove()) // Output: 7
}
C++
#include <iostream>
#include <vector>
#include <stdexcept>
class MaxHeap {
private:
std::vector<int> heap;
void percolateUp(int index) {
int parentIndex = (index - 1) / 2;
while (index > 0 && heap[index] > heap[parentIndex]) {
std::swap(heap[index], heap[parentIndex]);
index = parentIndex;
parentIndex = (index - 1) / 2;
}
}
void percolateDown(int index) {
int size = heap.size();
int largest = index;
while (true) {
int left = 2 * largest + 1;
int right = 2 * largest + 2;
if (left < size && heap[left] > heap[largest]) {
largest = left;
}
if (right < size && heap[right] > heap[largest]) {
largest = right;
}
if (largest != index) {
std::swap(heap[index], heap[largest]);
index = largest;
} else {
break;
}
}
}
public:
bool isEmpty() const {
return heap.empty();
}
int getMax() const {
if (isEmpty()) {
throw std::runtime_error("Heap is empty");
}
return heap[0];
}
int getSize() const {
return heap.size();
}
void insert(int value) {
heap.push_back(value);
percolateUp(heap.size() - 1);
}
int remove() {
if (isEmpty()) {
throw std::runtime_error("Heap is empty");
}
if (heap.size() == 1) {
int maxValue = heap[0];
heap.pop_back();
return maxValue;
}
int root = heap[0];
heap[0] = heap.back();
heap.pop_back();
percolateDown(0);
return root;
}
};
int main() {
MaxHeap maxHeap;
maxHeap.insert(10);
maxHeap.insert(4);
maxHeap.insert(9);
maxHeap.insert(2);
maxHeap.insert(7);
std::cout << "Max element peek: " << maxHeap.getMax() << std::endl; // Output: 10
std::cout << "Max element: " << maxHeap.remove() << std::endl; // Output: 10
std::cout << "Max element: " << maxHeap.remove() << std::endl; // Output: 9
maxHeap.insert(5);
std::cout << "Max element: " << maxHeap.remove() << std::endl; // Output: 7
return 0;
}
Rust
pub struct MaxHeap {
heap: Vec<i32>,
}
impl MaxHeap {
// Create a new empty MaxHeap
pub fn new() -> Self {
MaxHeap { heap: Vec::new() }
}
// Check if the heap is empty
pub fn is_empty(&self) -> bool {
self.heap.is_empty()
}
// Get the maximum element from the heap (root)
pub fn get_max(&self) -> Option<i32> {
self.heap.first().copied()
}
// Get the size of the heap
pub fn get_size(&self) -> usize {
self.heap.len()
}
// Insert a value into the heap
pub fn insert(&mut self, value: i32) {
self.heap.push(value);
self.percolate_up(self.heap.len() - 1);
}
// Remove and return the maximum element from the heap
pub fn remove(&mut self) -> Option<i32> {
if self.is_empty() {
return None;
}
if self.heap.len() == 1 {
return self.heap.pop();
}
let root = self.heap[0];
self.heap[0] = self.heap.pop().unwrap();
self.percolate_down(0);
Some(root)
}
// Percolate an element up the heap
fn percolate_up(&mut self, index: usize) {
let mut index = index;
while index > 0 {
let parent_index = (index - 1) / 2;
if self.heap[index] > self.heap[parent_index] {
self.heap.swap(index, parent_index);
index = parent_index;
} else {
break;
}
}
}
// Percolate an element down the heap
fn percolate_down(&mut self, index: usize) {
let size = self.heap.len();
let mut index = index;
loop {
let left = 2 * index + 1;
let right = 2 * index + 2;
let mut largest = index;
if left < size && self.heap[left] > self.heap[largest] {
largest = left;
}
if right < size && self.heap[right] > self.heap[largest] {
largest = right;
}
if largest != index {
self.heap.swap(index, largest);
index = largest;
} else {
break;
}
}
}
}
fn main() {
let mut max_heap = MaxHeap::new();
max_heap.insert(10);
max_heap.insert(4);
max_heap.insert(9);
max_heap.insert(2);
max_heap.insert(7);
println!("Max element peek: {:?}", max_heap.get_max()); // Output: Some(10)
println!("Max element: {:?}", max_heap.remove()); // Output: Some(10)
println!("Max element: {:?}", max_heap.remove()); // Output: Some(9)
max_heap.insert(5);
println!("Max element: {:?}", max_heap.remove()); // Output: Some(7)
}
Output
Max element peek: 10
Max element: 10
Max element: 9
Max element: 7
Using the heap push (insertion new element) we can create a heap if we are getting elements. In case we already have an array then we can convert it into a heap using Heapify method. We will discuss this later while learning about when and why to use Heapify.
| Operation | Worst Case |
|---|---|
| Get max | O(1) |
| Delete | O(log n) |
| Insert | O(log n) |
For full implementation to create heap from an array using heapify check this -