Binary tree traversals

Category: Data Structures
Tags: #datastructures#binary-tree

Binary tree traversals can be done by Depth-first traversal and Breadth-first traversals or Level order traversal. Preorder traversal, Inorder traversal and Postorder traversal are part of the Depth-first search.

Introduction to binary trees

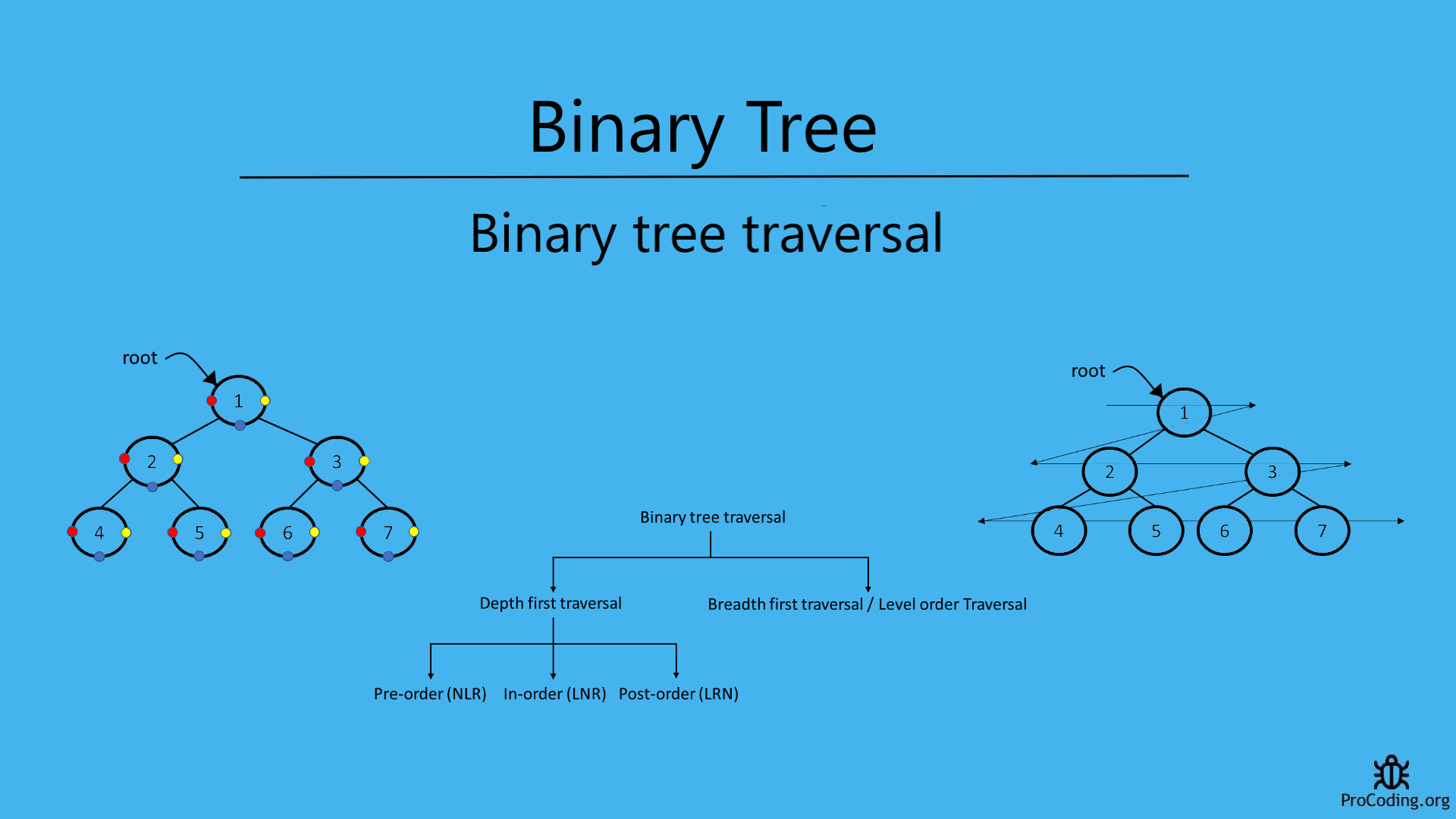
Table of contents

Traversal of tree means visiting each node once in a tree data structure.

Traversal of other data structures like array, linked list are sequential i.e., a praticular sequence is defined but sequential traversal of tree is not possible.

Types of tree traversals

Following are the types of traversal of a binary tree.

Linked List node

  • N - Root
  • L - Left
  • R - Right

These are the types of binary tree traversals

  • Depth first traversal
    • Preorder traversal
    • Inorder traversal
    • Postorder traversal
  • Breadth first traversal / Level order traversal

Depth first search

These tree traversals are known as depth first traversal because these traversal algorithms traverse the deepest node first and nodes at same level later.

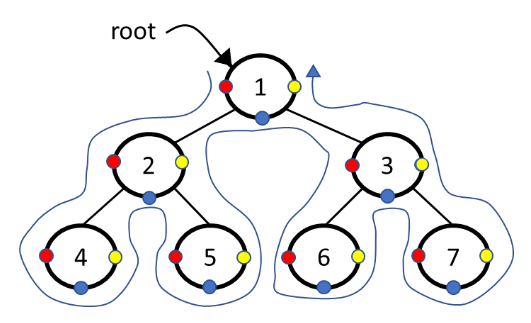
Linked List node

  1. Preorder (Root, Left, Right): 1, 2, 4, 5, 3, 6, 7
  2. Inorder (Left, Root, Right): 4, 2, 5, 1, 6, 3, 7
  3. Postorder (Left, Right, Root): 4, 5, 2, 6, 7, 3, 1

Breadth first search / Level order traversal

Level order traversal algorithm traverse the nodes at same level first and then traverse the nodes at next level.

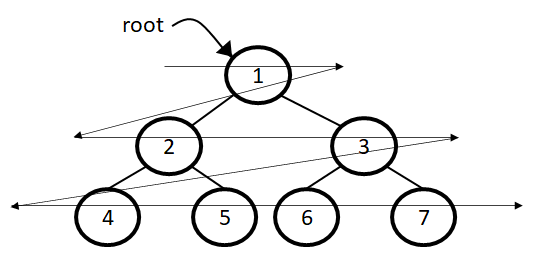
Linked List node

Breadth first search / Level order traversal: 1, 2, 3, 4, 5, 6

Preorder traversal

  1. Print the data of the current node
  2. Traverse the left subtree
  3. Traverse the right subtree

Recursive

Python
def pre_order(root):
    if root:
        print(root.data)
        pre_order(root.left)
        pre_order(root.right)
JavaScript
function preOrder(root) {
  if (root) {
    console.log(root.data);
    preOrder(root.left);
    preOrder(root.right);
  }
}

Iterative

For iterative traversal we have to use an extra stack data structure.

Python
def pre_order(root):
    if root:
        stack = []
        stack.append(root)
        while stack:
            node = stack.pop()
            print(node.data)
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
JavaScript
function preOrder(root) {
  if (root) {
    const stack = [];
    stack.push(root);
    while (stack.length > 0) {
      node = stack.pop();
      console.log(node.data);
      if (node.right) {
        stack.push(node.right);
      }
      if (node.left) {
        stack.push(node.left);
      }
    }
  }
}

Inorder traversal

  1. Traverse the left subtree
  2. Print the data of the current node
  3. Traverse the right subtree

Recursive

Python
def in_order(root):
    if root:
        in_order(root.left)
        print(root.data)
        in_order(root.right)
JavaScript
function inOrder(root) {
  if (root) {
    inOrder(root.left);
    console.log(root.data);
    inOrder(root.right);
  }
}

Iterative

For iterative traversal we have to use an extra stack data structure.

Python
def in_order(root):
    if root:
        stack = []
        node = root
        while stack or node:
            if node:
                stack.append(node)
                node = node.left
            else:
                node = stack.pop()
                print(node.data)
                node = node.right
JavaScript
function inOrder(root) {
  if (root) {
    const stack = [];
    node = root;
    while (stack.length > 0 || node) {
      if (node) {
        stack.push(node);
        node = node.left;
      } else {
        node = stack.pop();
        console.log(node.data);
        node = node.right;
      }
    }
  }
}

Postorder traversal

  1. Traverse the left subtree
  2. Traverse the right subtree
  3. Print the data of the current node

Recursive

Python
def post_order(root):
    if root:
        post_order(root.left)
        post_order(root.right)
        print(root.data)
JavaScript
function postOrder(root) {
  if (root) {
    postOrder(root.left);
    postOrder(root.right);
    console.log(root.data);
  }
}

Iterative

For iterative traversal we have to use an extra stack data structure.

Python
def post_order(root):
    if root:
        visited = set()
        stack = []
        node = root
        while stack or node:
            if node:
                stack.append(node)
                node = node.left
            else:
                node = stack.pop()
                if node.right and not node.right in visited:
                    stack.append(node)
                    node = node.right
                else:
                    visited.add(node)
                    print(node.data)
                    node = None
JavaScript
function postOrder(root) {
  if (root) {
    const visited = new Set();
    const stack = [];
    node = root;
    while (stack.length > 0 || node) {
      if (node) {
        stack.push(node);
        node = node.left;
      } else {
        node = stack.pop();
        if (node.right && !visited.has(node.right)) {
          stack.push(node);
          node = node.right;
        } else {
          visited.add(node);
          console.log(node.data);
          node = null;
        }
      }
    }
  }
}

Level order traversal

In these kind of traversal, nodes of each level are traversed first and then next level will be traversed sequentially from left to right.

Recursive

Python
def level_order(root):
    h = height(root)
    for i in range(1, h+1):
        level_order_traverse(root, i)
  
def level_order_traverse(root , level):
    if root is None:
        return
    if level == 1:
        print(root.data)
    elif level > 1 :
        level_order_traverse(root.left , level-1)
        level_order_traverse(root.right , level-1)

def height(root):
    if root is None:
        return 0
    return max(height(root.left), height(root.right)) + 1
JavaScript
function levelOrder(root) {
  const h = height(root);
  for (let i = 1; i <= h; i++) {
    levelOrderTraverse(root, i);
  }
}

function levelOrderTraverse(root, level) {
  if (root == null) {
    return;
  }
  if (level == 1) {
    console.log(root.data);
  } else if (level > 1) {
    levelOrderTraverse(root.left, level - 1);
    levelOrderTraverse(root.right, level - 1);
  }
}

function height(root) {
  if (root == null) {
    return 0;
  }
  return Math.max(height(root.left), height(root.right)) + 1;
}

Iterative

For iterative traversal we have to use an extra queue data structure.

Python
import queue           
def level_order(root):
    if root:
        q = queue.Queue()
        q.put(root)
        node = None

        while not q.empty():
            node = q.get()
            print(node.data)
            if node.left:
                q.put(node.left)
            if node.right:
                q.put(node.right)
JavaScript
function levelOrder(root) {
  if (root) {
    const q = [];
    q.push(root);
    node = null;

    while (q.length > 0) {
      node = q.shift();
      console.log(node.data);
      if (node.left) {
        q.push(node.left);
      }
      if (node.right) {
        q.push(node.right);
      }
    }
  }
}

Implementation of tree traversals

Recursive

Python
class Node:
    def __init__(self, data):
        self.left = None
        self.data = data
        self.right = None

# pre order traversal
def pre_order(root):
    if root:
        print(root.data)
        pre_order(root.left)
        pre_order(root.right)

# in order traversal
def in_order(root):
    if root:
        in_order(root.left)
        print(root.data)
        in_order(root.right)

# post order traversal
def post_order(root):
    if root:
        post_order(root.left)
        post_order(root.right)
        print(root.data)

# level odrer traversal
def level_order(root):
    h = height(root)
    for i in range(1, h+1):
        level_order_traverse(root, i)
  
def level_order_traverse(root , level):
    if root is None:
        return
    if level == 1:
        print(root.data)
    elif level > 1 :
        level_order_traverse(root.left , level-1)
        level_order_traverse(root.right , level-1)

def height(root):
    if root is None:
        return 0
    return max(height(root.left), height(root.right)) + 1

root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
JavaScript
class Node {
  constructor(data) {
    this.left = null;
    this.data = data;
    this.right = null;
  }
}

// pre order traversal
function preOrder(root) {
  if (root) {
    console.log(root.data);
    preOrder(root.left);
    preOrder(root.right);
  }
}

// in order traversal
function inOrder(root) {
  if (root) {
    inOrder(root.left);
    console.log(root.data);
    inOrder(root.right);
  }
}

// post order traversal
function postOrder(root) {
  if (root) {
    postOrder(root.left);
    postOrder(root.right);
    console.log(root.data);
  }
}

// level order traversal
function levelOrder(root) {
  const h = height(root);
  for (let i = 1; i <= h; i++) {
    levelOrderTraverse(root, i);
  }
}

function levelOrderTraverse(root, level) {
  if (root == null) {
    return;
  }
  if (level == 1) {
    console.log(root.data);
  } else if (level > 1) {
    levelOrderTraverse(root.left, level - 1);
    levelOrderTraverse(root.right, level - 1);
  }
}

function height(root) {
  if (root == null) {
    return 0;
  }
  return Math.max(height(root.left), height(root.right)) + 1;
}

const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);

console.log("Pre order traversal");
preOrder(root);
console.log("nIn order traversal");
inOrder(root);
console.log("nPost order traversal");
postOrder(root);
console.log("nLevel order traversal");
levelOrder(root);

Output



Pre order traversal

1

2

4

5

3

6

7



In order traversal

4

2

5

1

6

3

7



Post order traversal

4

5

2

6

7

3

1



Level order traversal

1

2

3

4

5

6

7

Iterative

Python
class Node:
    def __init__(self, data):
        self.left = None
        self.data = data
        self.right = None

# pre order traversal
def pre_order(root):
    if root:
        stack = []
        stack.append(root)
        while stack:
            node = stack.pop()
            print(node.data)
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)

# in order traversal
def in_order(root):
    if root:
        stack = []
        node = root
        while stack or node:
            if node:
                stack.append(node)
                node = node.left
            else:
                node = stack.pop()
                print(node.data)
                node = node.right

# post order traversal
def post_order(root):
    if root:
        visited = set()
        stack = []
        node = root
        while stack or node:
            if node:
                stack.append(node)
                node = node.left
            else:
                node = stack.pop()
                if node.right and not node.right in visited:
                    stack.append(node)
                    node = node.right
                else:
                    visited.add(node)
                    print(node.data)
                    node = None

# level odrer traversal
import queue           
def level_order(root):
    if root:
        q = queue.Queue()
        q.put(root)
        node = None

        while not q.empty():
            node = q.get()
            print(node.data)
            if node.left:
                q.put(node.left)
            if node.right:
                q.put(node.right)

root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)

print('Pre order traversal')
pre_order(root)
print('\nIn order traversal')
in_order(root)
print('\nPost order traversal')
post_order(root)
print('\nLevel order traversal')
level_order(root)
JavaScript
class Node {
  constructor(data) {
    this.left = null;
    this.data = data;
    this.right = null;
  }
}

// pre order traversal
function preOrder(root) {
  if (root) {
    const stack = [];
    stack.push(root);
    while (stack.length > 0) {
      node = stack.pop();
      console.log(node.data);
      if (node.right) {
        stack.push(node.right);
      }
      if (node.left) {
        stack.push(node.left);
      }
    }
  }
}

// in order traversal
function inOrder(root) {
  if (root) {
    const stack = [];
    node = root;
    while (stack.length > 0 || node) {
      if (node) {
        stack.push(node);
        node = node.left;
      } else {
        node = stack.pop();
        console.log(node.data);
        node = node.right;
      }
    }
  }
}

// post order traversal
function postOrder(root) {
  if (root) {
    const visited = new Set();
    const stack = [];
    node = root;
    while (stack.length > 0 || node) {
      if (node) {
        stack.push(node);
        node = node.left;
      } else {
        node = stack.pop();
        if (node.right && !visited.has(node.right)) {
          stack.push(node);
          node = node.right;
        } else {
          visited.add(node);
          console.log(node.data);
          node = null;
        }
      }
    }
  }
}

// level order traversal
function levelOrder(root) {
  if (root) {
    const q = [];
    q.push(root);
    node = null;

    while (q.length > 0) {
      node = q.shift();
      console.log(node.data);
      if (node.left) {
        q.push(node.left);
      }
      if (node.right) {
        q.push(node.right);
      }
    }
  }
}

const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);

console.log("Pre order traversal");
preOrder(root);
console.log("\nIn order traversal");
inOrder(root);
console.log("\nPost order traversal");
postOrder(root);
console.log("\nLevel order traversal");
levelOrder(root);

Output



Pre order traversal

1

2

4

5

3

6

7



In order traversal

4

2

5

1

6

3

7



Post order traversal

4

5

2

6

7

3

1



Level order traversal

1

2

3

4

5

6

7
Author - Abhishek Kumar