Number of leaf nodes in a binary tree
Those nodes in the tree which don't have any child are known as leaf nodes i.e., A node is a leaf node if both left and right child nodes of it are null. To find the number of leaf nodes in a binary tree, we have to traverse each node and in the tree and check if the current node is a leaf node or not and count them one by one.
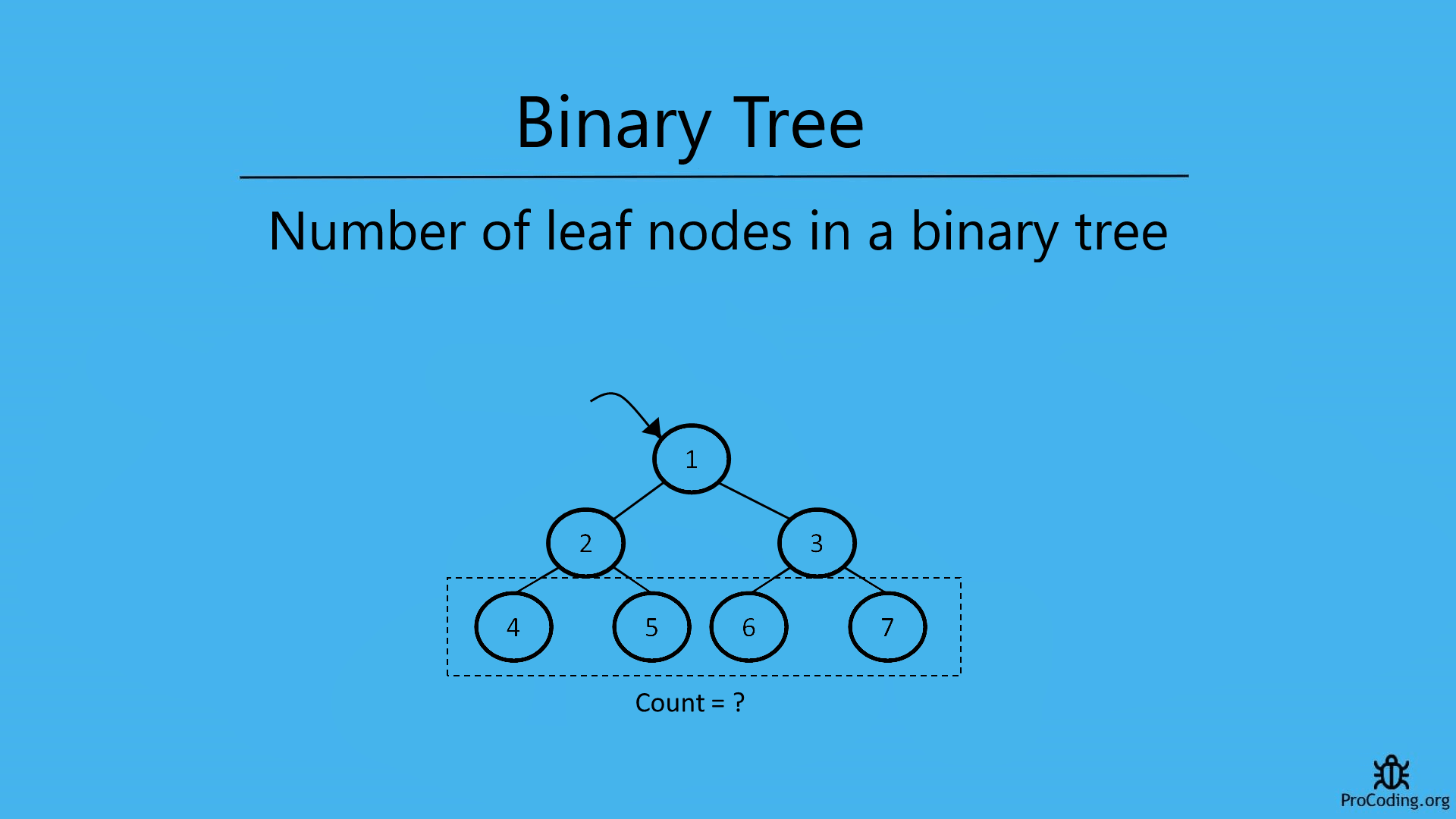
To find the number of leaf nodes in a binary tree or other trees, we have to traverse each node and in the tree and check if the current node is a leaf node or not and count them one by one.
Leaf nodes in a binary tree
Those nodes in the tree which don't have any child are known as leaf nodes.
A node is a leaf node if both left and right child nodes of it are null.
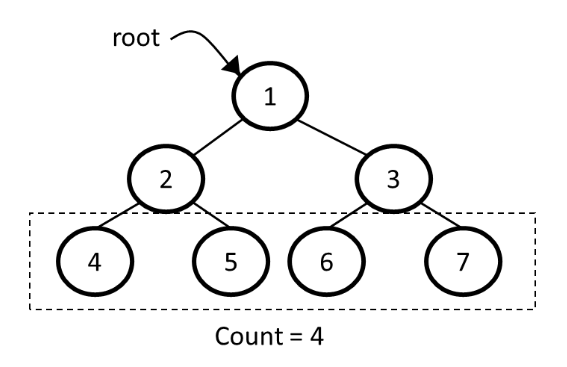
So, to count all the leaf nodes we have to traverse each node in the tree and count all those nodes which are not having any child i.e, both the children are null.
Example -
Input:
1
/ \
2 3
/ \ / \
4 5 6 7
Output: 4
We can solve this problem in two ways-
Recursive solution
For recursive solution we have to check each node one by one recursively as we have done in binary tree recursive traversal and count the nodes which are not having any child. Other types of traversal can also be used.
Algorithm
Leaf_Count(root)
1. if root is null then
2. return 0
3. if root->left is null and root->right is null then
4. return 1
5. else
6. return Leaf_Count(root->left) + Leaf_Count(root->right)
Python
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def leaf_count(root):
if root is None:
return 0
if root.left is None and root.right is None:
return 1
else:
return leaf_count(root.left) + leaf_count(root.right)
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print(leaf_count(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function leafCount(root) {
if (!root) return 0;
if (!root.left && !root.right) return 1;
else return leafCount(root.left) + leafCount(root.right);
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
console.log(leafCount(root));
Output
4
Iterative solution
For iterative solution, we have to traverse each node in level order and count the nodes which are not having any child.
Algorithm
Leaf_Count(root)
1. if root is null then return 0
2. queue.enqueue(root)
3. count = 0
4. while queue is not empty
5. node = queue.dequeue()
6. if node->left is null and node->right is null then
7. count = count + 1
8. else
9. if node->left is not null then
10. queue.enqueue(node->left)
11. if node.right is not null then
12. queue.enqueue(node->right)
13. return count
Python
import queue
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def leaf_count(root):
if root is None:
return 0
q = queue.Queue()
q.put(root)
count = 0
while not q.empty():
node = q.get()
if node.left is None and node.right is None:
count = count + 1
else:
if node.left:
q.put(node.left)
if node.right:
q.put(node.right)
return count
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print(leaf_count(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function leafCount(root) {
if (!root) return 0;
q = [];
q.push(root);
let count = 0;
while (q.length > 0) {
const node = q.shift();
if (!node.left && !node.right) count++;
else {
if (node.left) q.push(node.left);
if (node.right) q.push(node.right);
}
}
return count;
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
console.log(leafCount(root));
Output
4
Time complexity: The time complexity of both of these solution will be O(n) because we are just traversing each element of node one by one.