Maximum in Binary tree
Find the maximum element in a Binary tree using recursion or iterative solution. For example, a binary tree contains the following elements- 1, 2, 3, 4, 5, 6, 7 Here the maximum element will be 7.
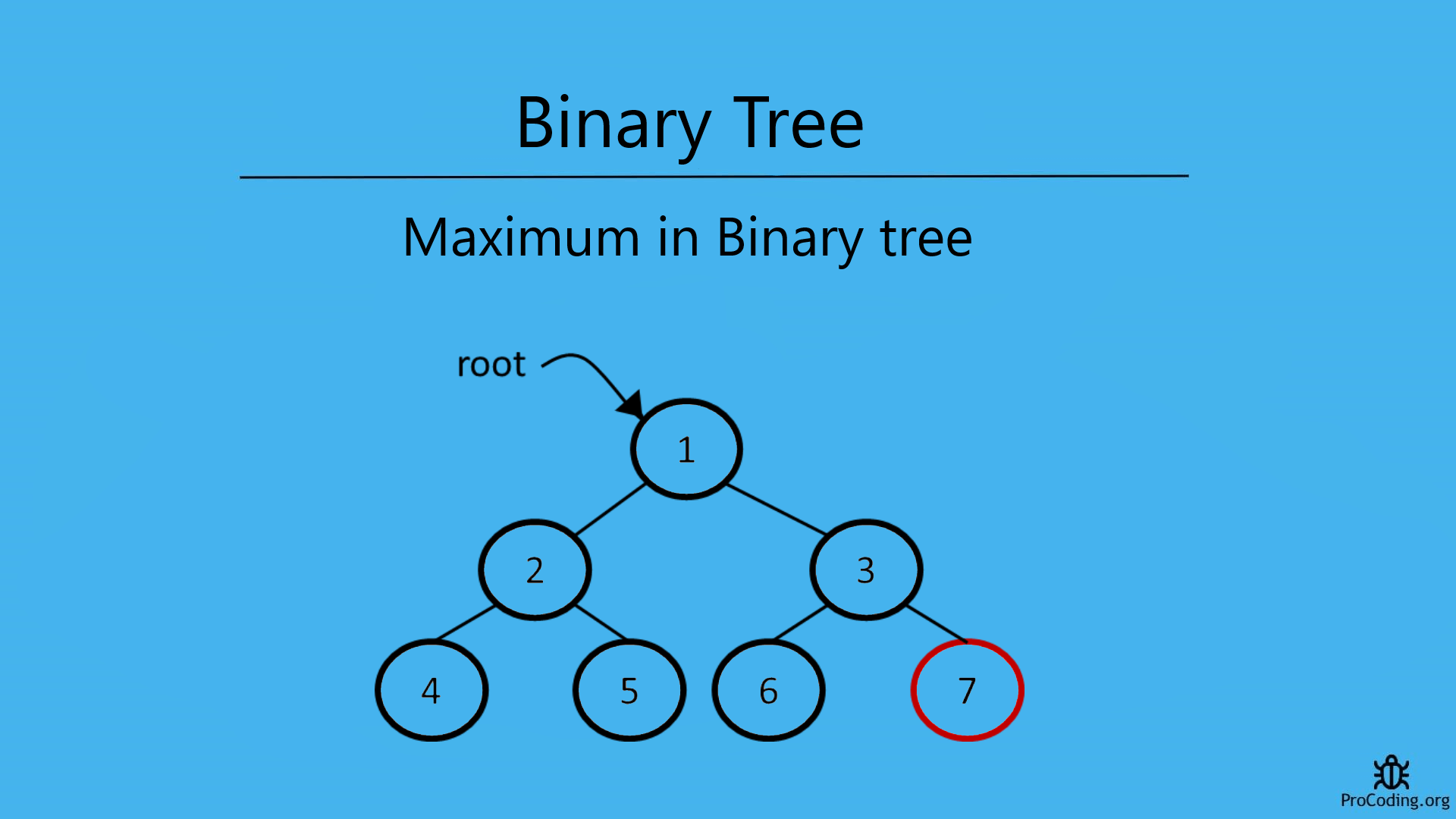
In a Binary Tree, to find the maximum element we have to traverse each element and check if an element higher than the current one is available then assign it as the maximum element. In the same way, we can find the minimum element too.
We can solve this problem in two ways-
Recursive solution
For recursive solution we have to check each node one by one recursively as we have done in binary tree recursive traversal.
Python
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def find_max(root):
if root is None:
return float('-inf')
max_val = root.data
left_val = find_max(root.left)
right_val = find_max(root.right)
if left_val > max_val:
max_val = left_val
if right_val > max_val:
max_val = right_val
return max_val
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print(find_max(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function findMax(root) {
if (root == null) {
return Number.NEGATIVE_INFINITY;
}
let maxVal = root.data;
leftVal = findMax(root.left);
rightVal = findMax(root.right);
if (leftVal > maxVal) {
maxVal = leftVal;
}
if (rightVal > maxVal) {
maxVal = rightVal;
}
return maxVal;
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
console.log(findMax(root));
Output
7
Iterative solution
For iterative solution, we have to traverse each node in level order and find the maximum by comparision.
Python
import queue
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def find_max(root):
if root:
max_val = root.data
q = queue.Queue()
q.put(root)
while not q.empty():
node = q.get()
if node.data > max_val:
max_val = node.data
if node.left:
q.put(node.left)
if node.right:
q.put(node.right)
return max_val
else:
return None
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
print(find_max(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function findMax(root) {
if (root) {
const q = [];
q.push(root);
node = null;
let maxVal = root.data;
while (q.length > 0) {
node = q.shift();
if (node.data > maxVal) {
maxVal = node.data;
}
if (node.left) {
q.push(node.left);
}
if (node.right) {
q.push(node.right);
}
}
return maxVal;
} else {
return null;
}
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
console.log(findMax(root));
Output
7
By using similar logic, we can also find the minimum element in a binary tree.
Time complexity: The time complexity of both of these solution will be O(n) because we are just traversing each element of node one by one.