Diameter of a Binary tree
The diameter of a tree is the number of nodes on the longest path between two leaves in the tree. Here, we will try to find the diameter of a binary tree using an unoptimized solution first and then we will try to find out the optimized solution using dynamic programming and in linear time.
Diameter of a Binary tree
The diameter of a tree is the number of nodes on the longest path between two leaves in the tree.
Consider the following example where more than on diameter path is possible because both the paths are having same distance or same number nodes.
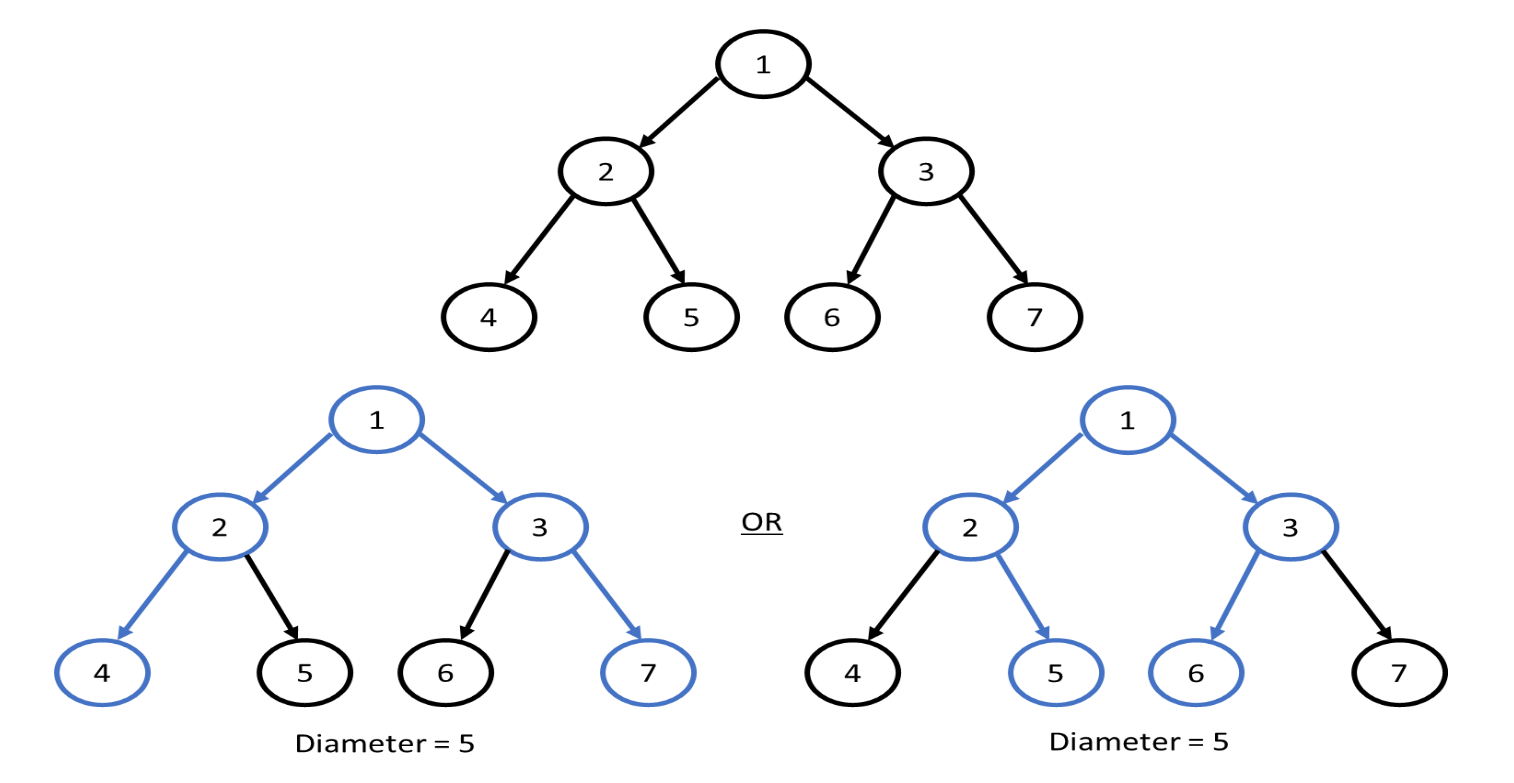
Consider another example where only a unqiue diameter of tree is possible.
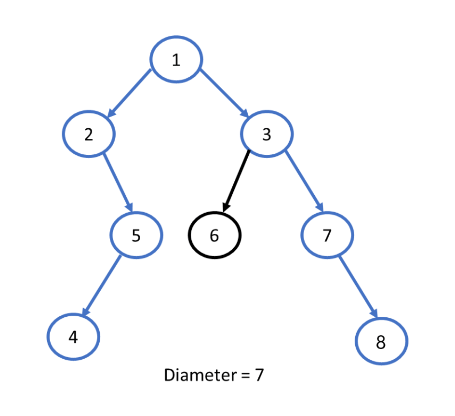
But it is not possible that the diameter of a tree always passes through the root node.
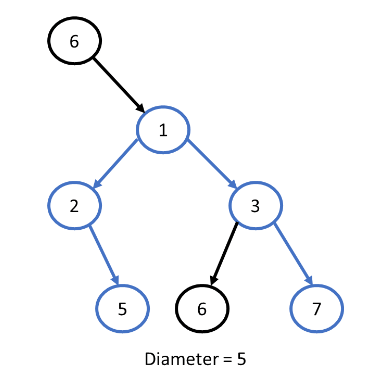
To find the diameter of a single node of a binary tree we have to find height of left sub tree then height of right sub tree and then add 1 to this i.e., diameter = left_child_height + right_child_height + 1.
Similarly, we have to find the diameter of each node in the binary tree and compare them together. The node having maximum diameter will be the height of the binary tree.
Example -
Input:
1
/ \
2 3
/ \ / \
4 5 6 7
Output: 5
Solution
For the solution, we have to traverse each node and find the height of each node then compare its height with other nodes at the end return the maximum height of the node that will be the diameter of the binary tree.
Algorithm
Height(root)
1. if root is null
2. return 0
3. return max(Height(root.left), Height(root.right)) + 1
Diameter(root)
1. if root is null
2. return 0
3. left_height = Height(root.left)
4. right_height = Height(root.right)
5. left_diameter = Height(root.left)
6. right_diameter = Height(root.right)
7. return max(
left_height + right_height + 1,
max(left_diameter, right_diameter)
)
Python
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def height(root):
if root is None:
return 0
return max(height(root.left), height(root.right)) + 1
def diameter(root):
if root is None:
return 0
lheight = height(root.left)
rheight = height(root.right)
ldiameter = diameter(root.left)
rdiameter = diameter(root.right)
return max(lheight + rheight + 1, max(ldiameter, rdiameter))
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(13)
root.right.right = Node(12)
print(diameter(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function height(root) {
if (root == null) return 0;
return Math.max(height(root.left), height(root.right)) + 1;
}
function diameter(root) {
if (root == null) return 0;
let lheight = height(root.left);
let rheight = height(root.right);
let ldiameter = diameter(root.left);
let rdiameter = diameter(root.right);
return Math.max(lheight + rheight + 1, Math.max(ldiameter, rdiameter));
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(13);
root.right.right = new Node(12);
console.log(diameter(root));
Output
5
Time complexity: The time complexity of this solution is O(n2) because we are calculating height and diameter of same node again and again which is not an optimized solution.
Optimized solution: Dynamic programming
We can solve this problem in linear time by traversing the tree in postorder. We will traverse the tree from the bottom and we already know the height of leaf node is 0. For upper nodes, we will simply increase the count by 1 and store the height of each node and further we can use height to calculate the diameter. This is how we can avoid the calculation of height again and again and retrieve the pre-calculated values.
Basically, we will be using Dynamic programming with memoization to find solution to this problem in linear time.
Algorithm
Get_Diameter(root)
1. if root is null
2. return 0, diameter
3. left_height, ldiameter = get_diameter(root.left, diameter)
4. right_height, rdiameter = get_diameter(root.right, diameter)
5. max_diameter = left_height + right_height + 1
6. diameter = max(ldiameter, rdiameter, max_diameter)
7. return max(left_height, right_height) + 1, diameter
Diameter(root)
1. diameter = 0
2. return Get_Diameter(root, diameter)[1]
Python
class Node:
def __init__(self, data):
self.left = None
self.data = data
self.right = None
def get_diameter(root, diameter):
if root is None:
return 0, diameter
left_height, ldiameter = get_diameter(root.left, diameter)
right_height, rdiameter = get_diameter(root.right, diameter)
max_diameter = left_height + right_height + 1
diameter = max(ldiameter, rdiameter, max_diameter)
return max(left_height, right_height) + 1, diameter
def diameter(root):
diameter = 0
return get_diameter(root, diameter)[1]
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(13)
root.right.right = Node(12)
print(diameter(root))
JavaScript
class Node {
constructor(data) {
this.left = null;
this.data = data;
this.right = null;
}
}
function getDiameter(root, diameter) {
if (root == null) return [0, diameter];
let [leftHeight, lDiameter] = getDiameter(root.left, diameter);
let [rightHeight, rDiameter] = getDiameter(root.right, diameter);
maxDiameter = leftHeight + rightHeight + 1;
diameter = Math.max(lDiameter, rDiameter, maxDiameter);
return [Math.max(leftHeight, rightHeight) + 1, diameter];
}
function diameter(root) {
let diameter = 0;
return getDiameter(root, diameter)[1];
}
const root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(13);
root.right.right = new Node(12);
console.log(diameter(root));
Output
5
Time complexity: The time complexity of this solution is O(n).